오늘은 Linear Discriminant Analysis(LDA)에 대한 수식적 이해를 돕도록 하겠다.
참고 : 머피의 머신러닝 1, CPSC 540
0. optional - 사전 지식
0-1. prior, posterior, likelihood
prior, posterior, likelihood에 대해 샘플 데이터 D, 학습하고 싶은 파라미터 θ를 기반으로 정리하면 다음과 같다.
- prior : P(θ)
- posterior : P(θ|D)
- likelihood : P(D|θ)
- posterior ~= prior * likelihood (by baysian)
이번엔 데이터가 피쳐 x와 라벨 y로 구성되어 있다 가정하자. 그러면 식이 다음과 같이 바뀔 수 있다. 아래와 같이 수식을 접근하게 되면 라벨 y의 클래스(c)가 달라질 때마다 분포가 달라질 수 있는 '조건(condition)'을 가정할 수 있게 된다.
- prior over class : P(y = c ; θ)
- class posterior : P(y | x; θ)
- class conditional density : P(x | y=c; θ)
오늘 글에서는 class posterior를 posterior로 줄여 쓸 예정이다.
0-2. Gaussian
Gaussian을 log로 옮긴다면 식을 다음과 같이 풀 수 있다. 우선 데이터 x가 평균이 u고 분산이 ∑인 가우시안 분포를 따른다고 가정하자.
- P(x|θ) = N(x| u, ∑)
이때 Log P(x|θ)는 아래와 같이 표현된다.
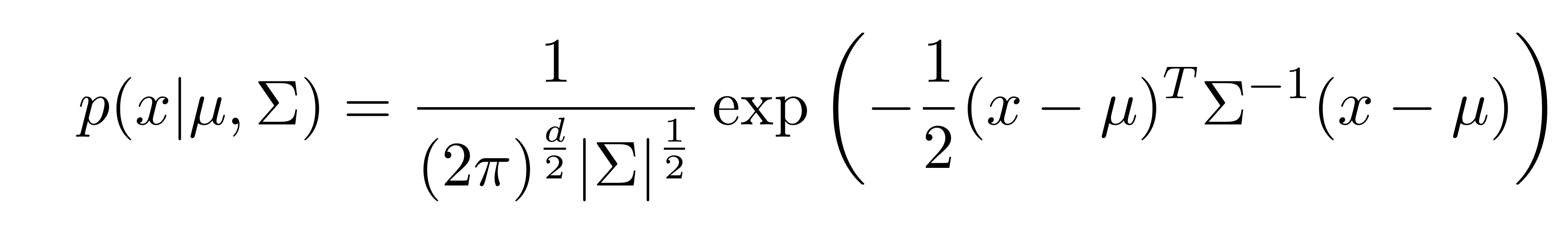
가우시안을 log로 나타내서 식을 풀 수 있음을 알았다. 그리고 마침 P(x|θ)를 보니 딱 Likelihood다. 우린 이제 가우시안 분포를 지니는 log likelihood를 구할 수 있게 됐다!
0-3. MLE
Gaussian에서 MLE를 구할 때 최적화된 prior, 평균, 분산은 다음과 같다.
- prior : Nc / N

0-4. Logistic Regression
a = Wx + b 를 만족하는 linear 함수가 있다고 가정한다. 이 함수는 predictor로 작동하며, 요 함수를 최적화하는 것이 Logistic Regression의 미션이다.

posterior 수식은 y가 binary일 때는 sigmoid, 그렇지 않을 때는 softmax 형태가 된다.
| binary - sigmoid | multinomial -softmax |
 |
|
 |
Linear Discriminant Analysis (LDA)
1. Discriminant Model의 이해
분류기를 크게 두가지로 분류하라고 한다면 생성(generative) 모델과 판별(Discriminative) 모델로 나눌 수 있을 것이다. 생성 모델은 말 그대로 라벨 y가 있을 때 x에 대해 생성하는 방법론이고, 판별 모델은 x에 대해서 y를 예측하는 방법론이다.
이를 정리하자면 생성 모델은 likelihood 기반, 판별 모델은 class posterior 기반이라 볼 수 도 있다.
| 생성모델 (Generative Classifier) | 판별 모델 (Discriminative Classifier) |
| likelihood 기반 | class posterior 기반 |
| p(x | y=c;θ) | p(y | x;θ) |
판별 모델은 class posterior를 구하는 분류 모델이다.(밑에서부터는 class posterior를 posterior로 나타내겠다.) 이때 클래스 y가 c로 지정되어 있다고 생각해 보자. 이를(posterior) 수식으로 나타내면 아래와 같이 (class conditional density) * (prior over class) 의 형태로 나타낼 수 있다. (posterior ~= prior * likelihood였음을 기억하자. optional 참고.)
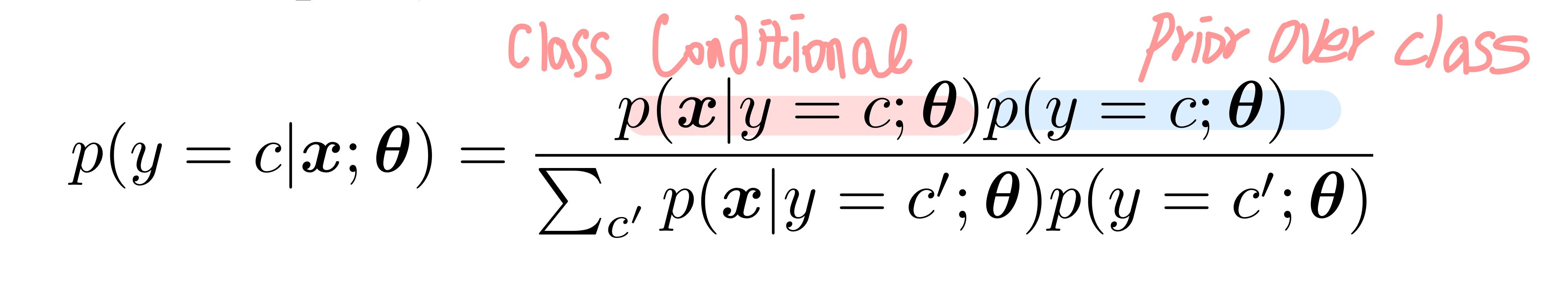
LDA는 이름에서도 알 수 있다시피 판별 모델에 속한다. 위 수식에서 posterior를 구할 때 class conditional density(p(x | y=c;θ))가 사용되었다. LDA는 이 class conditional density가 가우시안, 혹은 베이시안을 따르고 posterior를 선형함수(ex. wx +b) 로 나타낼 수 있는 방법론이다.
2. Decision Boundary로 보는 LDA
class conditional density가 가우시안일 때를 가정해서 위의 판별 모델을 나타내보자. 우선 class conditional density를 Gaussian으로 나타내면 다음과 같다.
- 이는 y=c일 때(class conditional), 즉 u_c, ∑_c를 분포의 특정 가우시안을 따르는 x를 구하는 식이다. y에 라벨이 c1, c2, c3가 있다면 y=c1, y=c2, y=c3일 때의 가우시안이 각각 있을 것이다.

posterior는 베이시안에 따라 prior * likelihood로 나타낼 수 있으므로, 우리가 구하고 싶은 class posterior는 다음과 같다. 이때의 π는 prior P(y=c)를 의미한다.

2-1. Quadratic decision boundaries ( == Quadratic Discriminant Analysis. QDA)
위 수식에서 우리는 Gaussian 분포를 따르는 x가 있을 때 y가 class c일 확률인 posterior p(y=c|x,θ)를 구했다. 여기에 log를 붙여서 log posterior를 붙이면 아래와 같이 나타낼 수 있다. (optional의 Gaussian 참고)
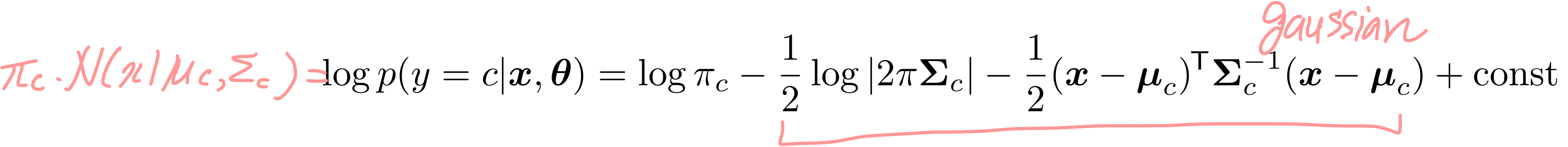
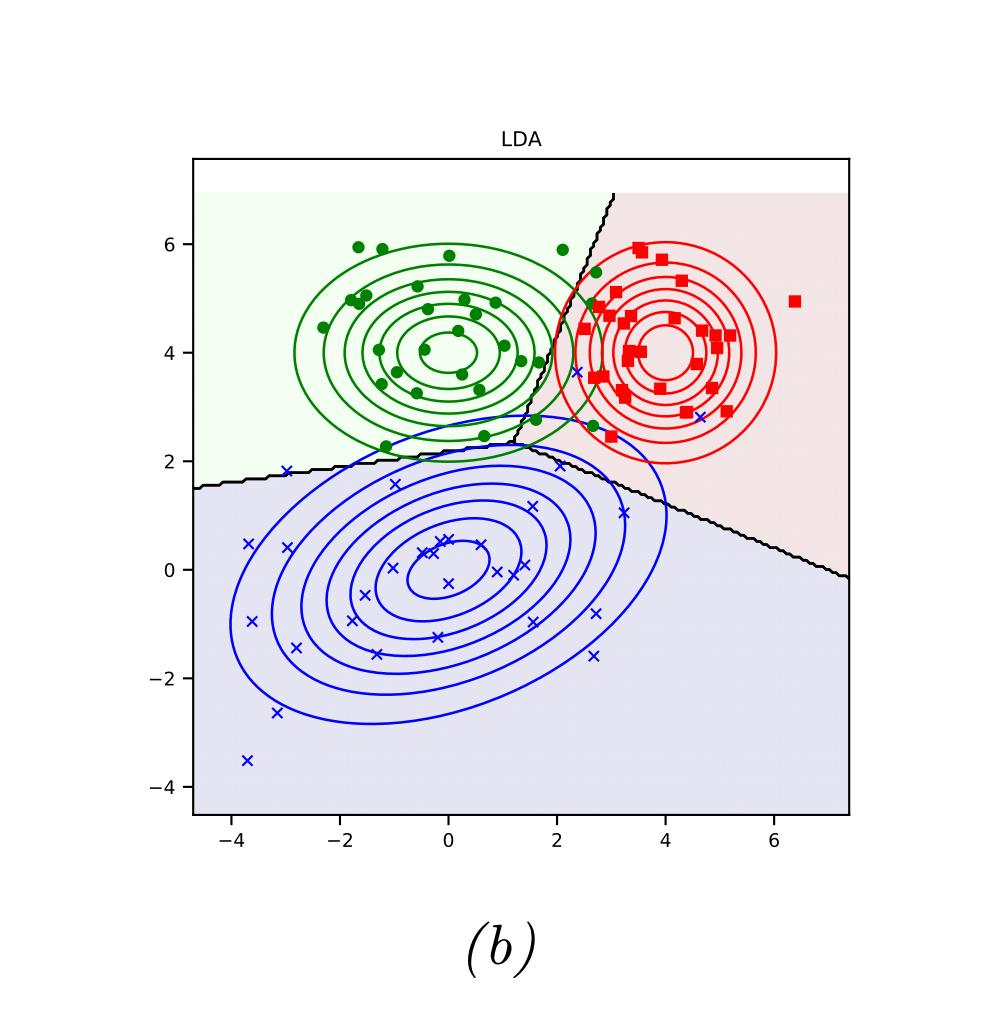
이 수식을 우리는 Discriminant Function, 즉 판별 함수로 지칭한다. 왜그럴까? 이 수식을 그림으로 나타내면 알 수 있다. 특정 클래스 c에 대해서 그려진 log posterior는 해당 클래스 c를 판별하기 위한 영역을 친 것과 같은 결과를 보인다.
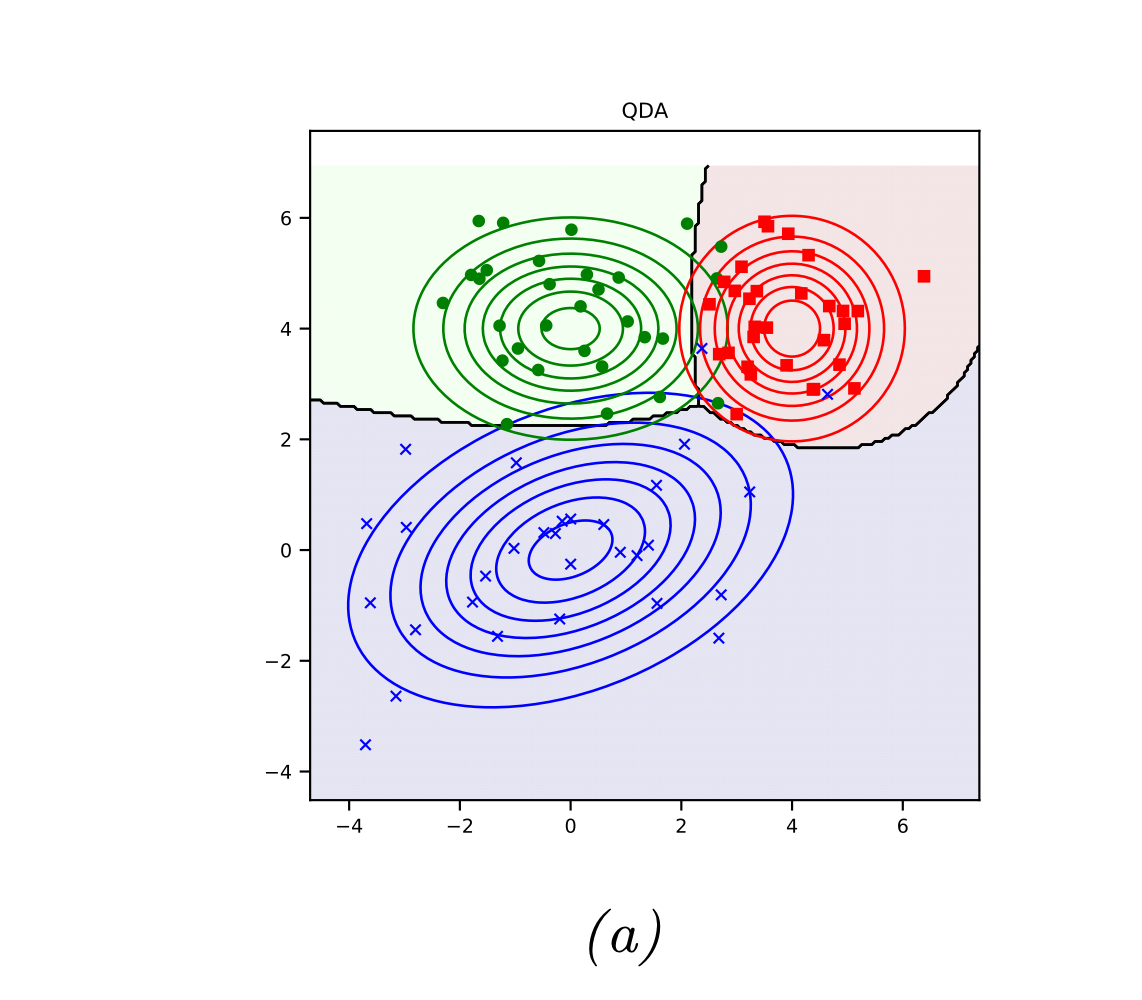
2-2. Linear Decision Boundaries (== Linear Discriminant Analysis. LDA)
위 QDA는 각 클래스 c에 대해서 다들 다른 분산과 평균을 가진 가우시안이 있다는 가정 하에 진행되었다. 하지만 만약에 모든 클래스 c들이 다 같은 분산을 가지고 있다면? 오늘 주제인 LDA가 된다.
QDA에서 사용한 log posterior 수식을 다시 가져와보자.

LDA의 가정이라면(모든 클래스 c들이 다 같은 공분산을 가지고 있음) 이 수식에서 모든 y=c에 대해 ∑_c 값은 동일하게 된다. x에 대한 식으로 볼 때 ∑를 상수로 봐도 된다는 의미다.
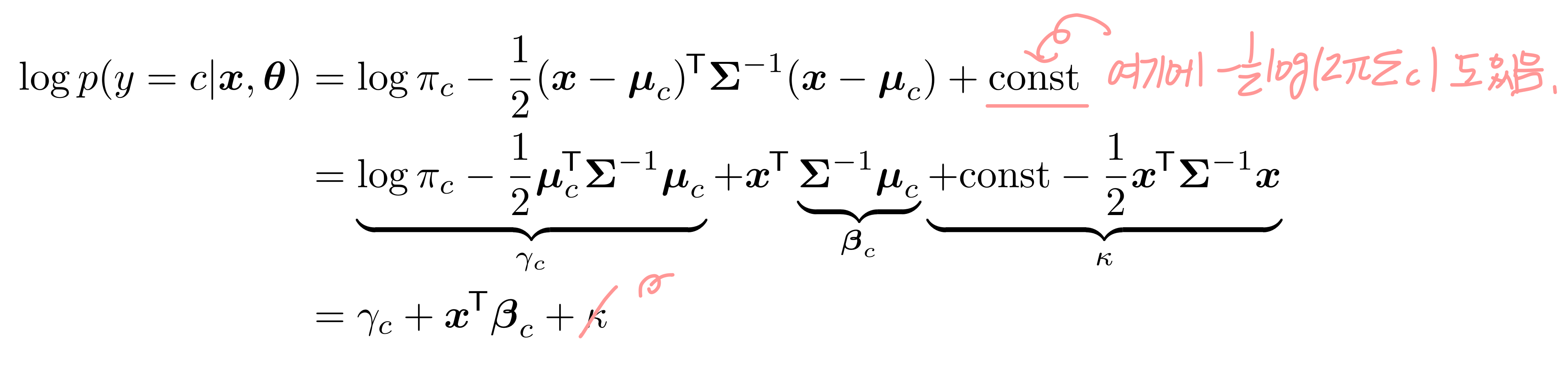
오호라, c를 기준으로 식을 정리해 보니 식이 간단하게 정리가 됐다. 이걸 보니 마치 x*w + b 꼴이지 않는가? 수식을 그림으로 나타내면 아래와 같다.
- 마지막 상수인 k는 c를 기준으로 했을 때 상수이기 때문에 날아간다.
2-3. GDA(LDA) Model Fitting
이제 LDA를 최적화하는 방법에 대해 얘기해보자. 가우시안 데이터를 fitting 하기 때문에 우리가 최적화하고 싶은 변수는 u, ∑로 볼 수 있다. Maximum Likelihood Estimate(MLE)를 통해 최적화한다면 각 변수의 최적값들은 각각 아래를 따를 것이다. 이때 N은 학습 데이터의 수, Nc는 y==c를 만족하는 데이터의 수이다.

수식을 봤을 때 u와 ∑ 모두 데이터 수 N에 대해 값이 달라질 수 있음을 확인할 수 있다. MLE가 오버피팅에 취약하단 사실을 이전 글에서 다뤘을 거 같은데, 비슷한 맥락이다. 데이터 수가 적으면 정확한 u, ∑를 얻을 수 없을 것이다.
2-4. Model Fitting 2 - Metric Learning
log likelihood를 통해 모델을 최적화하는 MLE가 있는가 하면, LDA에서는 수식의 생김새를 봤을 때 하나 더 선택지를 가질 수 있다. 바로 posterior가 가장 큰 값을 갖는 y=c를 구하는 것이다. (log p(y=c1 |x), log p(y=c2|x) ... 중 어떤 값이 제일 클까?)
세 번째로 log posterior 수식을 재탕해 보자.
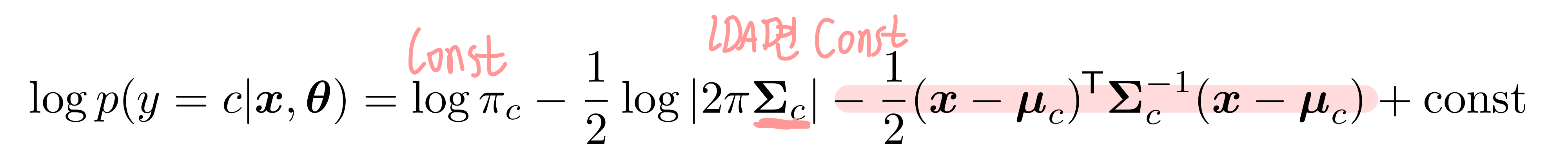
이때 우리가 구하고픈 y(x)는 c에 대한 식을 남겼을 때 정리가 다음과 같이 정리할 수 있다.

Metric Learning에서 기틀이 되는mhalanobis distance 수식만 남게 된다. c의 평균과 데이터 x 간의 거리를 구하는 함수가 됐다. x 와 c의 중심이 가까우면 y는 c일 확률이 높을 것이고, 그렇지 않으면 x와 c의 중심의 거리는 멀기를 기대한다.
3. LDA vs Logistic Regression
LDA를 Logistic Regression 수식으로도 나타낼 수 있다. 들어가기 전에 LDA와 Logistic Regression의 차이점을 먼저 찝어보자면 다음과 같다. posterior의 형태가 P(y= c | x, θ)임을 기억하자.
- LDA : LDA의 목적은 θ에 해당하는(==prior) Gaussian 파라미터 u, ∑를 fitting하는 것이다. posterior를 fit 하는 건 그다음 과제.
- Logistic : postrior를 fit 함으로써 θ를 최적화하고자 한다.
뭔가 전후관계가 묘하게 다른 것을 알 수 있다. LDA는 θ를 찾은 후 posterior를 구하려 하고 Logistic Regression은 posterior 최적화를 통해 최적의 θ를 찾고자 한다. 이 관계를 염두에 두고 이제 수식을 전개해보자.
2-2에서 LDA의 log posterior 결과가 아래와 같았음을 기억하자.
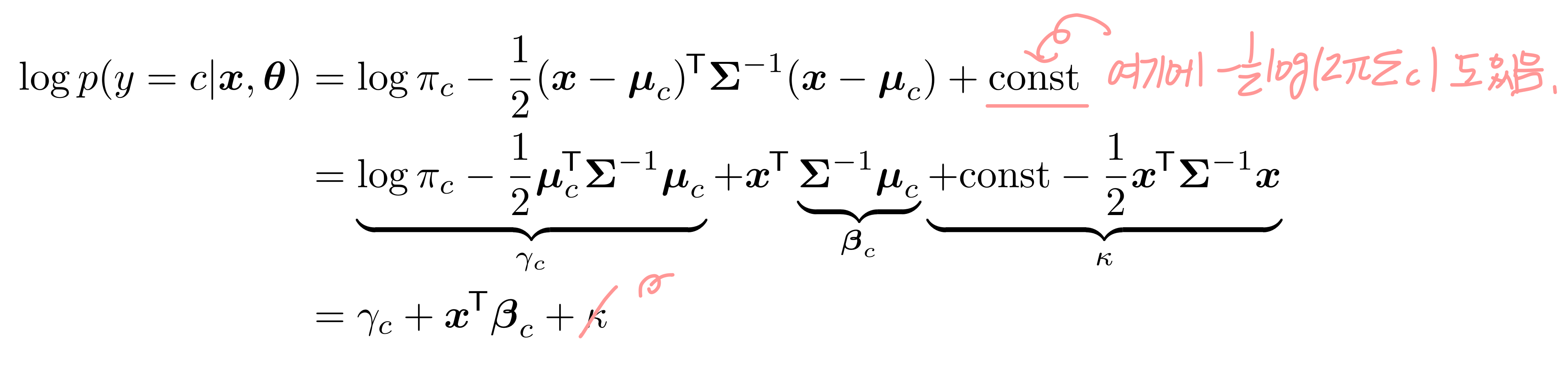

이를 linear predictor(y=wx + b)로 생각하고 logistic regression의 linear 자리에 넣어보자. 아래 식에서 w_c = [γ, β]을 의미한다.

이번 예시는 binary로 가정한다. y=0 또는 y = 1만 존재하므로 아래와 같이 식이 정리된다. 아래 식의 σ는 sigmoid를 의미한다.

γ, β에 다시 식을 대입해서 정리하면 놀랍게도 logistic function과 같은 형태로 정리가 된다.


마치며
오늘은 Linear Discriminant Analysis(LDA)에 대해 알아보았다.
- LDA는 이 class conditional density가 가우시안, 혹은 베이시안을 따르고 posterior를 선형함수(ex. wx +b) 로 나타낼 수 있는 방법론이다.
- Discriminant Classifier는 posterior를 최적화한다. ~ P(y= c | x, θ)
- Gaussian Discriminant Analysis(GDA)는 prior가 Gaussian 분포를 따른다. ~ P(x) = N(x|u_c, ∑_c)
- GDA에서 모든 c들에 대해 공분산 값이 같으면 Linear Discriminant Analysis(LDA)이다. ~ ∑_c == constant
- LDA를 최적화하는 방법은 Gaussian 기반 모델을 최적화하는 방법을 쓰면 된다. ~ MLE, MAP 등등
- LDA 수식을 정리하면 Metric Learning 나 Logistic Regression 이 될 수 있다.
LDA가 오버피팅의 우려가 있기 때문에 이를 극복하기 위한 트릭들이 여럿 있다. (MAP를 쓰거나, 분산값에 제한을 두거나 등등) 그 중 하나가 Fisher's LDA이다. 원래는 이 글에서 다루려 했지만 너무 늘어지는 것 같아 잘랐다.
'머신러닝 > 기초 머신러닝' 카테고리의 다른 글
| EM(Expectation-Maximization) 알고리즘의 완벽한 기초 (4) | 2023.08.13 |
|---|---|
| [짧] KNN(K Nearest Neighbor) 분류모델 이론 (0) | 2023.08.06 |
| Lagrange Multiplier 이론 정리 (0) | 2023.07.29 |
| Exponential Family 개념 정리 (0) | 2023.06.24 |
| MLE 완벽 개념 (2) | 2023.05.29 |

