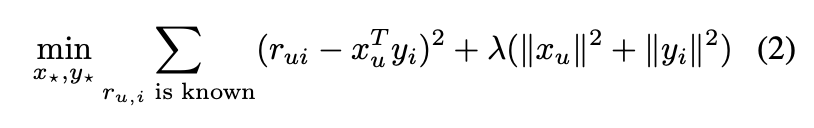lu의 머신러닝 개발자로 살아남기

오늘은 지난 포스트 Matrix Factorization(MF)와 ALS에 이어서 Factorization Machine(FM)에 대한 기초를 다뤄볼 예정이다. 

MF의 핵심은 user 와 item 간 interaction에 대한 하나의 행렬 A이 있을 때, 이를 user 벡터 U와 item 벡터 V로 행렬분해를 한 형태로 가져갈 수 있다. U와 V의 dot product가 user-item 간 유사도를 나타내는 것으로 이해할 수 있었다. 

FM도 하고자 하는 바는 유사하다. user들과 item 이 주어졌을 때 user에게 무슨 아이템을 추천해야하는지를 알고 싶다. 하지만 비슷한 이름에 비해 과정은 사뭇 다르다. 

• 참고 paper : Factorization Machines. 2010

1. PREDICTION UNDER SPARSITY

FM은 ranking을 예측하는 regression 문제로 접근하지 않고 classification task로 풀고자 한다.  user-item-score 쌍이 anti symmetric이라 postive sample로만 학습한다. (참고: item a가 b보다 항상 ranking이 높다면 b가 a보다 높을 일은 없다.) 

FM도 highly sparse data를 가정한다. figure1을 보면 user와 item feature를 concat해 하나의 feature로 활용한다. 이는 오직 user-item interactioin을 value로 표현했던 MF와는 다르다. 

fig1의 x(1) feature를 예시로 설명하면, A user가 TI 영화를 봤고, 지금까지 영화들에는 다음과 같은 평점을 주었으며, TI 영화는 13개월차에 봤고(논문에선 2009년부터 1개월씩 +1 카운트한다), 직전에 A가 평점메긴 영화들에는 무엇이 있었는지를 나타낸다. target y(1)은 A user가 TI item에 준 rate다. 5라고 되어있으니 5점이다.

여러 피쳐들을 활용해서 ranking 예측 모델을 설계하고 있음을 알 수 있다. 

2. FACTORIZATION MACHINES (FM)

FM에선 degree d = 2 로 설정해 dot product한다. feature x1, x2가 있다고 가정했을 때 이 둘을 dot product 함으로써 두 피쳐간의 인터렉션을 활용하는 것이다. 아래 Equation에서의 마지막 항에 해당한다. v는 따라서 x_i와 x_j의 인터렉션에 대한 weight가 된다.  w0은 global bias (~= b), w_i는 feature weight를 의미한다. 수식 생김새를 보면 알듯이 gradient descent(GD)를 쓸 수 있다.

( 수식 내 x는 위 fig1와 다르다! )

v는 자체로 k개의 factor를 가지고 있다. 만약 k가 충분히 크다면 어떤 interaction 행렬 W에 대해  W = V trans(V) 가 성립되는 V를 찾을 수 있다. 이러면 모든 피쳐들간의 상호작용을 V의 dot product로 나타낼 수 있게 될 수 있다. 하지만 인터렉션 자체가 sparse하기 때문에 고차원으로 나타내지 않고 k를 작게 해서 표현한다. 

그런데 metrix자체가 sparse하지 않았던가. x_i, x_j간 인터렉션을 잘 나타낼 수 있을까? 논문에선 이 문제를 factorization으로 해결한다. 

user A가 item ST에 대해 인터렉션한 적이 없다고 해보자. <v_A, v_ST> = 0 일까? 다른 유저들 B, C를 보니 item ST, SW을 둘다 본 적이 있다. 여기서 v_ST와 v_SW가 유사할 수 있다는 것을 캐치한다. 그래서 <v_A , v_ST> ~= <v_A, v_SW>로 근사할 수 있다.

그럼 이거 연산량은 괜찮을까? 직관적으로 보면 O(n**2) 일 것 같지만 실제 식을 풀어보면 다행히 O(k n)이다. 

이후 이 식을 regression, classification, ranking 등에서 쓸 때는 오버피팅 방지를 위해 R2 reg를 추가한다. 

Matrix and Tensor Factorization

MF은 FM의 피쳐를 x 하나만 썼을 때의 특이 케이스로 해석할수도 있다. fig1 에서 피쳐가 user, item 2가지만 있다고 가정하면 FM 수식이 다음과 같게 된다. 

이는 Matrix Factorization에서는 dot(u, v)를 구하는데, 이를 행렬이 아닌 스칼라 계산식으로 생각하면 위와 유사하게 된다. 

오늘은 Matrix Factorization(MF)와 Alternating Least Square(ALS)에 대해서 알아보고자 한다. 

참고: [paper] Collaborative Filtering for Implicit Feedback Datasets 

0. 선수 지식 

SVD 

Singular Value Decomposition(SVD)에 대해선 이전 포스트에서 자세히 다룬 적 있다. 

간략하게 정리해보면 SVD란 하나의 행렬을 고유행렬들로 분해하는 과정이다. A라는 행렬이 주어졌을 때 두개의 singular 행렬(U, V)과 특이값의 대각행렬(S) 곱 형태로 나타낼 수 있다. 이때 A가 대칭행렬이라면 분해된 singular 행렬은 eigen vector, eigen value와 같다. 

A = U S trans(V) 

1. Matrix Factorization

유저와 아이템 메트릭스가 있다고 가정해보자. 유저가 아이템과 인터렉션 한 값이 행렬로 채워진 상태, 예를 들어 유저수 1000만, 아이템 수 1만이라고 해보자. 유저-아이템 메트릭 A의 shape는 (10,000,000 , 10,000) 이 된다. 벌써 연산값이 어마어마하다. 

이를 SVD를 적용해서 특이값행렬 U, V로 짜개볼거다. U의 shape는 (10,000,000, r) V는 (10,000, r) 이다. r은 그럼 잠재적인 factor가 되는데, 벡터 U의 입장에서는 행렬 A에 대한 left singular vector이기 때문에 유저 row 별 임베딩으로 볼 수 있다. 

r이 의미하는 것은 결국 latent factor로, 상위 r개 rank에 대한 피쳐를 남겨둔 것이다. 

A = U S trans(V) 였다. 그러므로 다음과 같이 쪼갤 수 있다. 

빨간색 1번이 유저 임베딩, 빨간색 2번이 아이템 임베딩으로 이해할 수 있다. 여기서 대각행렬 S은 각 r 열들의 importance 가중치를 의미하기 때문에, 상대적인 유사도를 구할 때 스킵해도 되는 요소가 된다. 

따라서, np.dot(U, trans(V)) ~= 유저들의 아이템들에 대한 유사도가 될 수 있다. 1000만 by 1만 행렬연산을 안해도 되고, sparse vector에서 rank r로 압축되었기 때문에 표현력도 좋다. 

Matrix Factorization(MF)의 행렬분해를 통해 유저-아이템 유사도를 구할 수 있음을 보았다. 

2. MF와 ALS 

그러나 SVD를 사용하기 위해서는 어쨌든 행렬 A가 어느정도 값이 채워져 있어야 한다. 죄다 null이면 애초에 특이값을 분해하기 힘들테니 말이다. 1000만 유저와 1만 아이템에 대한 interaction을 행렬로 나타냈을 때 만약 1만 아이템이 대부분 cold item이라면 어떻게 할까? 

sparse metrix가 된다. 

SVD를 통한 MF에서 우리는 행렬 A를 U, S, V로 나타냈으며, U는 유저임베딩, V는 아이템 임베딩으로 이해할 수 있었다. 이때 우리가 추천에서 알고 싶은 유저와 아이템 간의 유사도는 U*V로 나타낼 수 있음을 알았다. 

이제 우린 ALS를 통해 sparse metrix A를 U와 V로 나타낸다. 이제 편의상 svd left singular vector였던 U는 P, svd의 right singular vector였던 V는 Q로 표현하겠다. 

유사도 ~= np.dot(P , trans(Q))

P와 Q를 알게 된다면 SVD에서처럼 유사도를 구할 수 있게 된다. 그럼 어떻게 P와 Q를 구할까? ALS에선 P를 고정한 후 Q를 업데이트하고, Q를 고정한 후 P를 업데이트하는 형식으로 P와 Q의 최적값을 찾는다. 그래서 이름이 Alternating Least Square다. 

A를 표현하는 것을 P와 Q 2개의 벡터로 하고자 한다. 따라서 objective function은 A와 P dot Q의 차를 loss term으로 둘 수 있다. 이는 선형회귀에서 잔차의 제곱을 최소화하고자 하는 Least Square와 유사하다. 식을 보니까 L2 loss와 유사하다.  그래서 이름이 Alternating Least Square 인가보다.

아래 식에서 r이 A, x와 y는 각각 P와 Q라고 볼 수 있다. 람다 항은 regularization term이다. 

L2 loss는 다른말로 MSE loss다. 딥러닝에서 회귀 문제를 풀 때 목적함수로 주로 쓰는 형태다. 그말은 즉 이 object function을 minimize하는 일을 Gradient Descent(GD)로 풀수도 있다는 말이다. 

하지만 우리는 ALS를 본다. row별 업데이트가 가능하기 때문에 대규모 데이터를 다룰 때 필요한 분산처리가 가능하기 때문이다.

위 term을 우리가 보기에 편하게 다시 써보면, 

minimize (A - np.dot(P, trans(Q))**2 + lambda (||P**2|| + ||Q**2||) 

ALS 컨셉 상 P를 계산할 때 Q는 상수취급을 받고, Q를 계산할 땐 P가 상수취급을 받는다. 따라서 P를 계산할 때는 Q 업데이트를 신경쓰지 않고 배치 업데이트가 가능할테고, 반대의 경우도 마찬가지다. 

ALS의 spark 라이브러리 함수는 다음과 같다. 

from pyspark.ml.recommendation import ALS

als = ALS(rank=10, seed=0) #rank ~= r을 의미한다. 상위 r개 피쳐까지로 압축할 것인가. 
als.setMaxIter(5) #몇번 학습할건지 


model = als.fit(df)

오늘 가져온 논문은 Deep Neural Networks for YouTube Recommendations 이다. 유튜브에서 2016년도에 낸 추천 알고리즘에 대한 내용이다. 

이 논문을 비롯한 여러 추천 시스템이 2 stage 양상을 띈다. 

저번에 다룬 구글의 wide&deep과도 유사한 점이 많다. 그럼 시작! 

1. Introduction 

딥러닝을 이용해서 추천하고싶어! 그러면서 풀고자 한 문제는 크게 세가지다. 

• Scale: 당시 16년도의 많은 추천 알고리즘들은 작은 스케일에선 괜찮은 효과를 내지만 유튜브같은 방대한 풀과 유저에서는 효과를 못봤다고 한다. 
• Freshness: 신규 업로드되는 유튜브 컨텐츠가 많기 때문에 최신성 유지와의 balance를 고려해야 한다. 추천에서의 exploration / exploitation 균형과 같다. 
• Noise: 컨텐츠의 메타데이터도 퀄리티가 좋지 않고, 유저 인터렉션에도 노이즈가 많다. 

당시 유튜브와 구글은 많은 문제를 딥러닝으로 해결하고자 하는 시도가 있었다고 한다. (추천 DL이 거의 전무했던 시기) 그래서 lesson learn에 좀 더 치중한 내용을 다루는 듯 하다. 

2. System Overview 

전체적인 아키텍처는 다음 figure 2와 같다. 크게 candidate generation과 ranking으로 나눌 수 있다. 

1) candidate generation에선 유저가 관심있을법한 컨텐츠들을 여기서 미리 선별한다. 

2) ranking 에서 보다 자세한 best recommendation이 이루어진다. 

candidate generation에서는 검색 retriever, CF 등 여러 소스를 같이 혼합해서 사용할 수 있다. 

3. CANDIDATE GENERATION

유저와 관련된 몇백개 정도의 비디오를 선별하는 단계다. 여기서 DNN extreme multitask classification 문제로 접근한다. 유저 벡터와 아이템(비디오) 임베딩이 input으로 주어질 때, 해당 아이템들 중 가장 볼법한 것을 분류 문제로 만든 것이다. 이때의 학습 라벨은 좋아요같은 explicit feedback이 아닌 시청시간(watches)을 통한 '완시'로 기준을 세웠다. 여기서 하고자 하는 건 기존 추천 시스템의 MF(Matrix Factorization)을 대체하는 것이다. 좋아요 등을 안쓴 이유는 사람들이 많이 안써서(~=sparse해서)라고 한다. 

아래 식은 softmax다. U는 유저 벡터, C는 컨텐츠 벡터다. 전형적인 분류 문제로 바뀌었다. 

많고 많은 컨텐츠들을 전부 분류모델에 태울 순 없으니 candidate sampling을 한다. 랜덤으로 선택한 negative 컨텐츠들도 학습에 사용하여 오버피팅을 방지한다. 

infer시엔 효율을 위해, 즉 시간 단축을 위해 softmax 대신 Nearest Neighbor 탐색, dot product로 후보 컨텐츠들을 선별한다. 

컨텐츠 임베딩은 word embedding으로 진행했다. 마찬가지로 유저임베딩에서도 유저가 시청한 컨텐츠들의 임베딩을 concat해서 dense vector를 생성했다. 그래서 figure3의 그려진 최하단 블록은 유저 임베딩을 나타낸 거다.

딥러닝을 MF 대신 사용하면서 이점은 categorical, continuous 피쳐도 모델에 input으로 주기 용이해졌단거다. 유저의 검색이력과 성연령 등등 다양한 피쳐를 input으로 사용한다. 

모델 학습시엔 컨텐츠 최신성을 고려하기 위해 비디오의 age도 같이 넣어준다. 컨텐츠가 업로드 후 빠르게 소모되는 패턴을 분석한 결과를 피쳐에 적용했다. 시간이 지날수록 컨텐츠의 인기도도 달라지기 때문에 training window를 도입하고 example age도 같이 넣어 학습한다. 서빙시에는 example_age == 0으로 주는데, 이는 컨텐츠의 가장 최신의 인기패턴을 반영하라는 것과 같다. 

추가로 모델이 exploit에 치중되지 않게 CF도 도입하고, 학습 편향이 특정 유저군에 집중되지 않도록 유저 당 학습셋을 고정했다. 

추천 피드를 검색 결과만 뜨게 하는 것도 지양할 수 있게 검색어 발생시점 데이터도 사용하지 않는다.  유저가 어느날 테일러 스위프트를 검색했다가 다시 나타났을 때, 테일러 스위프트와 관련된 컨텐츠만을 추천하는 것을 방지하기 위함이다. 

그리고 학습 라벨을 고르는 과정은 다음과 같이 이어지는 행동에서 추출한다. 유저의 시청이 플로우가 이어지는 다음 시청이었을 때만 해당 데이터를 정답셋으로 사용한다. 

유저 피쳐에선 본것 최근 최대 50개, 검색어 최근 50개를 함께 사용한다. 

4. RANKING

candidate generation과 유사하게 DNN 아키텍처를 차용했고 logistic regression으로 문제를 풀었다. 비디오들의 score를 메기는 단계다. 

피쳐로는 the traditional taxonomy of categorical and continuous/ordinal features을 사용했다. 특히 유저의 직전 컨텐츠들과의 interaction으로 이뤄졌다. 이 체널 컨텐츠를 얼마나 봤나, 특정 주제에 대한 컨텐츠를 최근 언제 봤나 등등, 그리고 generation에서 얻은 해당 컨텐츠의 점수도 같이 사용한다. 

churn(변화) 개념도 있다. 유저가 봤는데 지나친 컨텐츠에 대한 피쳐값을 추가해서, 자연스럽게 랭킹이 낮아질 수 있도록 한다. 

정황상 컨텐츠의 ID embedding은 lookup table을 사용했다고 하니 카테고리등의 text 임베딩도 녹였을 것으로 보인다. 이를 categorical 피쳐로 녹인듯하다.

추가로 continuous feature는 normalize해서 사용했다. quantile norm 후 루트를 씌웠다. 

아래 fig에서의 language embedding은, 자연어 language를 뜻하진 않아보인다. user language도 유저벡터를 의미하는 것으로 보인다.

모델은 (당연해보이지만) hidden layer를 더 둘수록 성능이 좋았다고 한다. 

5. CONCLUSIONS

AB 테스트에서 시청시간 지표가 개선됐다고 한다. 얼마나 개선됐는지 표는 없다. 

오랜만에 옛날(?) 논문을 가져왔다. 16년도에 구글에서 발표한 추천시스템 모델인 wide and deep 논문이다. 

구글 플레이스토어에서 사용되었고, 대규모 추천 시스템이 가져야하는 효율적인 서빙에 대해서도 고민한 내용이 담겨있다. 

간단하지만 강력한 wide&deep에 대해 알아보자. 

그럼 시작! 

1. Introduction

본 논문에서 추천의 범위는 '검색'에 대한 '랭킹' 추천이다. 1) given input을 Query로 정의하고, 2)해당 쿼리와 유사한 아이템(여기서는 플레이스토어니까 앱)들을 가져와서, 3) 의도에 맞게 랭킹을 메겨 내려준다. 

이 논문에서는 추천이 풀고자 하는 과제를 2가지로 정의했다. 

1. Memorization
   1. 유저가 이전에 한 행동, 즉 과거 데이터를 추천에 녹인다. 
   2. 과거 유저가 이런 행동을 했다는 걸 쿼리하는 예시를 보면 이해가 된다. (AND(user_installed_app=netflix, impres-sion_app=pandora”)) 
2. Generalization 
   1. 과거에 거의 발생하지 않았던 새로운 피쳐와 correlation을 찾는다. 과거에 기반하지 않기 때문에 추천 다양성을 의미하는듯 하다. 
   2. 유저의 조금 덜 뾰족한 피쳐들을 사용할 수 있다. AND(user_installed_category=video, impression_category=music)

Wide&Deep 이름의 유래를 알아보자. 

• Wide component 
  •  일반적으로 linear regression으로 푼다. 
  • 위 Memorization, Generalization에서의 AND 으로 가져온 피쳐들을 사용하는데(cross product) 당연하지만 장점은 유저의 특징을 모델에 녹일 수 있다는 거다. 
  • 그렇기에 단점은 train에 사용하지 않은 피쳐가 실제 infer에 나타났을 경우엔 취약하단 거다. 
  • -> Memorization > Generalization 
• Deep component 
  •  Factorized Machine(FM), DNN이 여기에 해당한다. 
  • 피쳐들을 dense embedidng화하기 때문에 일반화에 대해서는 Wide component에 비해 잘한다. 반면 query item metrix가 너무 sparse하거나 가져올 수 있는 피쳐들이 적다면 over generalization될 수 있다. 
  • -> Generalization > Memorization 

그래서 Wide&Deep은 DNN과 logistic regression을 합쳤다.  

2.RECOMMENDER SYSTEM OVERVIEW

추천시스템을 설명해둔 섹션인데, 간단히 요약해보겠다. 추천시스템을 크게 retriever와 ranker로 나눌 수 있다. 

유저 쿼리가 주어졌을 때 retrieval단계에서 추천할 후보 풀 아이템들을 가져온다. (모든 아이템들을 가져와서 ranking을 메기는 것은 온라인 추천에선 현실적으로 불가하다.) 

이후 ranker에서 유저 별 아이템풀들에 대한 랭킹을 메긴다. 

3. Wide & Deep Learning

아래 figure 1을 기준으로 보자. 맨 아래 하단은 sparse features, 위에서 AND 구문 안에 들어갔던 유저 또는 아이템 피쳐들이다. 

1. Wide Models에서는 이 피쳐를 그대로 logistic regression 등을 통해 output을 생성한다. 해당 feature들은 binary로 표현된다. 

(ex. lang=en, 성별=f -> {'en': 1, 'f': 1, 'm': 0, ...} 

2. 반면 Deep Model은 피쳐들을 dense embedding으로 만든다. 

3. 이 둘을 합친 Wide&Deep은 deep은 deep대로, wide는 wide대로 진행하되 마지막 layer에서 deep과 wide의 output을 합친다. 앙상블 모델인가 싶지만 joint training 을 한다. backpropagation은 같이 진행되기 때문. 

합칠 땐 weighted sum된 상태로 logistic regression을 사용한다. 아래 식에서 φ는 origin feature의 cross dot product, 즉 Wide에 해당한다. a는 Deep model의 final activation layer까지 통과한 벡터를 의미한다. w_wide와 w_deep은 각각 wide와 deep의 weight 가중치다. 

4. SYSTEM IMPLEMENTATION

data generation에서는 단어들은 categorical화 했고, continuous value는 min max 0, 1해서 quantile별로 값을 메기는 normalization을 진행했다. 

학습을 위한 model architecture는 다음과 같다. deep에서 relu를 3번이나 태운다.(hidden layer가 3개라는 뜻으로 보인다.) wide에서 사용한 피쳐는 유저가 아이템에 준 피드백들이 대상이다. 

학습 데이터는 500B개를 사용했다. 

5. Conclusion

wide보단 deep이, deep보단 deep&wide의 Acquisition Gain이 더 높았다. 

논문에서 리포트한 당시 peak 트래픽이 10 ms다.

키포인트는, DNN으로 랭킹 모델을 만들었지만, 유저의 피드백과 같이 memorization에 해당하는 부분은 Wide 모델로 보강을 해줬다는 거다. 

지난 포스트에서는 MAB와 Epsilon Greedy, Thompson Sampling에 대해서 정리했다. 이번에는 조금 더 진도를 나가서 LinUCB에 대해 알아보자. 

0. 사전 지식 

Contextual Bandit 

강화학습과 추천에서 Bandit은 어떤 것을 선택해야 최적의 값이 나올까를 고민한다. MAB(Multi Armed Bandit)는 여러가지 선택지 (arm. 또는 action)에서 최적의 reward를 가지는 것을 선택해야 한다.

contextual bandit은 MAB에서 context(상황)을 추가로 고려한다. 현재의 상황에 대한 피쳐가 있다고 가정했을 때(x_t), 이를 기반으로 action(a)을 선택하게 된다. 

• P(a | x_t) 

MAB에서 모든 상황을 동일하게 가정하고 최적의 reward를 고르는 것과는 다르다. 

1. LinUCB 

Lin

기존의 MAB에서 action이 가지는 reward 기댓값이 θ 였다면, context를 고려하기 시작하면 '해당 컨텍스트에서 action을 취할 확률'을 구해야 한다. 

이를 선형적(linear)으로 결합한다면 θ * x 으로 볼 수 있다. θ가 arm을 선택하기 위한 weight이 된다. 

UCB

UCB는 Upper Confidence Boundary를 뜻한다. 추천에서 exploration(탐험)과 exploitation의 적절한 균형을 찾는 일은 계속되어야 한다. 특정 arm(action)에 대해서 생각해보자. 

이 arm을 선택할 때 exploration의 관점은 일종의 불확실성이다. 

반면 exploitation은 이 선택을 함으로써 받게 될 reward(μ​)를 계산할 수 있다. 이는 평균 reward로 이해할 수 있다. 

특정 arm을 선택했는데 exploration으로 선택했든, exploitation으로 선택했든, 둘 다의 관점에서 얻을 수 있는 점수의 최대치(upper bound) 는 다음과 같이 UCB 수식으로 설계할 수 있다. 즉 이는 이 arm을 선택했을 때의 최대 reward 추정치다. 

위 수식에서 t는 시간, n_a(t)는 지금까지 이 arm을 선택한 횟수를 의미한다. exploration 항은 즉 arm을 선택한 적이 없을수록 커진다. 

LinUCB에서의 UCB

UCB 점수는 다음과 같이 정의된다.

1) exploitation reward μ​는 context x를 고려했을 때 선형적으로 θ * x 로 표현할 수 있었다.

• θ_a ⊤ ​x_t

2) exploration항은 해당 arm을 얼마나 많이 선택했었냐에 대한 항이었다. 이를 context x와 arm을 선택했던 컨텍스트들 x_t의 선택 유무 행렬 A를 활용해 정의할 수 있다. 

이때 A는 design matrix이다. 시점 s에 action a를 선택한 컨텍스트 피쳐 x에 대한 정보가 담겨있을 것이다.

• x_s​ = 시점 s에서 arm a가 선택되었을 때의 컨텍스트(feature) 벡터

x_s를 outer product 한걸 summation한 것은 피처별로 covariance를 포함한 상호관계를 더했다고 해석할 수 있다. 이 더한 값에 I를 더함으로써 cov 행렬을 완성했다. 

A의 역행렬은 공분산의 역수이기 때문에, t 시점의 정보들이 많다면 작은값을 나타낼 것이다. 여기에 현 컨텍스트 x_t를 곱한다면, x_t가 지금까지 action을 선택했던 feature중에서 얼마나 낯선 것인지 점수화할 수 있다. 

예시

예를 들어 현재 컨텍스트 피쳐가 2개라고 해보자. arm1을 선택했던 컨텍스트는 지금까지 총 2개 있었다고도 해보자.

• x_1 = [1 ; 2] (1x2dim) 
• x_2 = [0; 1] (1x2dim)

그럼 A_1 = x_1 x_1_t  + x_2 x_2_t + I 이므로

[1;2] [1;2]T + [0;1] [0;1]T + I 

[1 2            +  [0 0          + [1 0    == [2 2 

2 4]                0 1]              0 1]          2 6]

이다. 즉, A_1 == [2 2 ; 2 6] (2x2 dim) 

이의 역행렬을 계산한다면 [0.75−0.25​ ; −0.25 0.25​] (2x2dim)이다. 

여기에 현재 t의 컨텍스트 x_t의 첫번째 피쳐는 1, 두번째 피쳐는 1이라고 해보자. x_t = [1 ; 1] 

그럼 현 피쳐에서 arm1을 선택했을 때 exploration 점수는,

trans(x_t) * A_1 -1 * x_t  이므로

[1 1]  * [0.75 -0.25    * [1    

          -0.25 0.25]          1]

== 0.5다. 

물론 여기에 exploration 계수 α를 곱해줘야 한다. 

그러면 현재 arm 1 의 UCB점수는 다음과 같이 구해진다. 

• UCB_a1 = trans(θ_a1) *[1;1] +  α * 0.5 

여러 arm 중에서 UCB값이 가장 높은 arm을 선택하게 될 것이다. 선택한 arm의 reward에 따라서 현시점 t에서의 디자인 벡터 A도 업데이트되고, 예상 reward θ도 업데이트된다. (이때 θ는 linear regression으로 업데이트된다.)

오늘은 추천 알고리즘을 공부하면 많이 듣게 되는 기초, Multi Armed Bandit (MAB)에 대해서 알아보자. 그 중 Epsilon Greedy와 Tompson Sampling에 대해서 설명해보겠다. 

0. 기본 지식

exploration

이름 그대로 탐험을 의미한다. 추천할 때 새로운 아이템을 추천하는 등, 학습에 fitting되지 않는 미지의 영역을 새롭게 보여주는 개념으로 이해할 수 있다. 

아직 클릭이 적은 아이템이나, 기존 로직에 반영하지 않은 fresh 아이템을 노출하는 것이 여기에 해당한다. 그렇기에 매일 유저에게 비슷한 결의 아이템이 추천되는 것을 방지할 수 있다. 단, 당장의 reward는 낮을 수밖에 없다. 

exploitation 

데이터를 기반으로 해서 추천을 해주는 영역이다. 이미 쌓인 데이터 기반으로 확실한 reward를 보장할 수 있다. 

추천에서는 이 exploration과 exploitation의 균형을 잘 잡는 것이 중요하다.

MAB

여러개의 arm bandit 중 하나를 선택한다는 의미의 Multi Arm Bandit이다. 카지노 슬롯 머신을 생각하면 쉽다. 추천에서는 여러개의 액션(ex. 추천할 수 있는 아이템) 중 하나에 해당하는 슬롯 레버 Arm을 선택한다고 상상해보자. 

prior, posterior, likelihood

이전 포스트에서 다룬 적 있으나, 구글에서 글 안에 글 링크를 달면 싫어하는 것 같다. 자세한 건 내 블로그의 다른 글을 참고해주시면 된다. 

오늘 설명할 버전으로 기술하면 아래와 같다. 

• θ
  • 이 arm을 선택할 확률 
• prior: P(θ)
  • beta distribution 
• posterior : P(θ|D)
  • 업데이트된 성공 확률 분포 
• likelihood : P(D|θ)
  • 이 arm의 reward가 1또는 0

beta distribution

beta distribution은 다음과 같은 확률분포를 띈다.

여기서 MAB에 중요한 개념은 어떻게 beta distribution이 업데이트 되는지다. conjucate prior라고 가정했을 때,

posterior는

P(θ∣D) = k∼Beta(α+k,β+n−k)

이 된다. 즉, k가 "성공"일 때 알파값은 α +=k , 베타값은 β -=k 와 같이 업데이트 된다. 

1. epsilon greedy 

강화학습에서 나오는 개념이다. 지금까지의 가장 reward가 높은 아이템을 exploitation을 하지만, 일정한 비율 입실론(ε)에 대해서는 탐험 exploration을 한다.  

파이썬으로 간단하게 예시를 작성해볼 수 있다. 만약 0.3의 확률은 새로운 아이템을 '탐험' 시키고, 그렇지 않으면 reward가 가장 높은 아이템을 추천으로 선택하는 epsilon greedy 함수를 작성해보자. 

import numpy as np

# 먼저 유저에게 해당 아이템이 추천됐을 때 기대되는 reward를 얻는다. 
user_action_reward = [0, 0, 0.3 ,0.7, 1.0] #1명의 유저, 5개의 아이템에 대한 reward 


# epsilon greedy function 
def epsilon_greedy(rewards, epsilon = 0.3):
  if np.random.rand() < epsilon:
        # 랜덤하게 eps 확률에는 랜덤하게 데이터가 나간다. 
        choosen_idx = np.random.randint(len(rewards))
  else:
        # Exploit: choose the action with the highest Q-value
        choosen_idx = np.argmax(rewards)
  expected_reward = rewards[choosen_idx]
  return choosen_idx, expected_reward
  
epsilon_greedy(user_action_reward)

이론상 10번 중 3번은 가장 높은 1.0에 해당하는 index 4가 아닌 다른 아이템이 return된다. 

2. Tompson Sampling

epsilon-greedy가 일정한 확률대로 새로운 아이템을 return한다면, tompson sampling은 그 확률을 베이지안 (baysian) 에 기반한다. 그리고이 arm이 성공적인가 아닌가를 1 또는 0  으로 본다. 

posterior가 baysian이면 보통 conjucate (prior와 posterior가 유사한 확률분포를 따른다고 가정) prior는 beta distribution을 따른다. 

P(θ)가 beta-distribution일 때, baysian을 이용해서 학습한 arm bandit 알고리즘을 tompson sampling이라 할 수 있겠다. (실은 다른 conjucate prior를 사용해도 무방하다. 여기선 "보통" 자주 쓰이는 beta - baysian conjucate를 예시로 설명한다.)

베이시안에 따라 posterior는 다음과 같이

• Beta(α + 성공횟수, β + 실패횟수)

로 확률이 업데이트가 된다. 데이터 학습이 진행될수록 distribution의 파라미터인 α 값이 커지면서 탐험(exploration)보다 exploitation의 확률이 더 올라간다. 

이제 파이썬으로 구현해보자. 이번에도 각 아이템이 추천됐을 때의 reward를 데이터로 삼는다. 

먼저 arm을 선택하는 확률이다. 이는 계속 언급했듯이 prior 로 beta distribution 기반이다.

def select_arm(self):
        # 각 arm의 성공확률 θ 
        # P(θ) beta distribution 구하는 방법: np.random.beta(self.alphas[i], self.betas[i])
        samples = [np.random.beta(self.alphas[i], self.betas[i]) for i in range(self.num_arms)]
        return np.argmax(samples)

다음은 알파와 베타를 업데이트 해야한다. posterior는 해당 값에 성공 여부를 더해주면 된다. 

def update(self, chosen_arm, reward):
        #여기가 baysian. 
        # P(θ|a)는 likelihood. reward가 success threshold보다 큰지 아닌지 binary. 
        # P(θ)는 beta-distribution. 
        # P(a|θ)는 업데이트된 성공 확률 분포. (posterior) 
        if reward[chosen_arm] >= self.success_ths: 
            self.alphas[chosen_arm] += 1
        else:
            self.betas[chosen_arm] += 1

이제 코드를 합쳐보자. 

import numpy as np

class ThompsonSampler:
    def __init__(self, num_arms, success_ths): #num_arms: 현재 아이템 갯수 
        self.num_arms = num_arms
        self.alphas = np.ones(num_arms)  # successes
        self.betas = np.ones(num_arms)   # failures
        self.success_ths = success_ths

    def select_arm(self):
        # 각 arm의 확률 θ 
        # θ beta distribution 구하는 방법: np.random.beta(self.alphas[i], self.betas[i]) 
        samples = [np.random.beta(self.alphas[i], self.betas[i]) for i in range(self.num_arms)]
        return np.argmax(samples)

    def update(self, chosen_arm, reward):
        #여기가 baysian. 
        # P(θ|a)는 reward가 success threshold보다 큰지 아닌지 binary. 
        # P(θ)는 beta-distribution. 
        # P(a|θ)는 이 arm을 선택할 확률임. 
        if reward[chosen_arm] >= self.success_ths: 
            self.alphas[chosen_arm] += 1
        else:
            self.betas[chosen_arm] += 1

n_arms = 5 # 5개의 아이템으로 간주
success_ths = 0.7 # 추천 성공으로 간주하는 reward의 threshold 
smp = ThompsonSampler(n_arms, success_ths) 

trial = smp.select_arm()
print(f'current selected item idx: {trial}')
smp.update(trial, user_action_reward)
print(f'current alpha, beta distribution: {smp.alphas, smp.betas}')
## current selected item idx: 4
## current alpha, beta distribution: (array([1., 1., 1., 1., 2.]), array([1., 1., 1., 1., 1.]))

이를 계속해서 시도하면 높은 reward를 가진 arm에 따라 distribution도 수렴하는 것이다.