요즘 positional embedding은 결국 RoPE(Rotary Positional Embedding)가 짱을 먹은 것 같다. 이쯤에서 비교해보는 RoPE 와 일반 positional embedding.
어떤 관점에서 이 둘이 다르고, 그렇기 때문에 모델이 가지는 특징적 차이에 대해서 알아보자. 추가로 attention 이전과 이후 모델이 갖는 차이점도 정리해보겠다.
0. Attention 전과 후 LM 모델
Attention이 등장한 후에 Embedding의 종류에 Position Embedding이 추가되었다. BERT 등장 이전의 자연어모델을 생각해보면 LSTM, GRU, ELMo는 Recurrent NN (RNN) 을 사용했다.
당시 RNN의 한계는 명확했다.
- 연산을 순차적으로, sequence대로 해야 한다.
- gradient vanishing에 대한 두려움이 있다.
연산을 순차적으로 진행해야 하는 이유는 앞 토큰의 정보를 뒤 토큰에서 참고해야 하기 때문이었다. 그렇게 순차적으로 weight를 계산하다 보니, 뒤로 갈수록 앞에서 가져온 정보는 희석된다. gradient vanishing이 나타나는 것이다. 이를 해결하기 위해 일반 RNN을 진화시킨 ELMo(bidirectional 형태) 등이 나왔었다.
반면 Attention을 접목시킨 BERT를 보자. 파란색 네모 안을 들여다보면 토큰이 순차적으로 계산되지 않는다. 모든 토큰이 한번에 통으로 계산되는 것이다. 모든 토큰을 한번에 보기 때문에 긴 문장이어도 문맥을 파악할 수 있게 되었다.
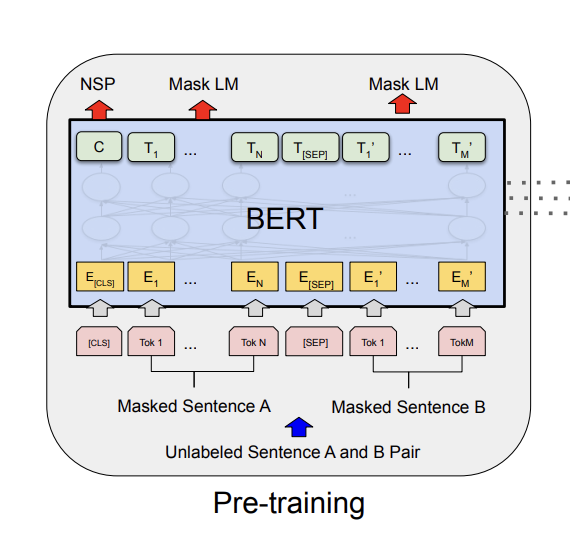
RNN처럼 토큰을 순차적으로 계산하는게 아니라 통으로 계산한다면 단점이 뭘까?
- 모든 토큰을 한번에 계산하기 때문에 computational cost가 늘어난다. 원래는 (하나의 토큰 x 하나의 토큰) 연산을 n개의 토큰만큼 이어서 진행했다면 Attention은 (n개의 토큰 x n개의 토큰) 연산이 되는 것이다. O(n**2) 이다.
- 이 토큰이 어디에 있던 건지를 모른다.
1번 단점은 그럴 수 있다고 치자. 2번은 무슨 뜻일까? 'I love you so much' 라는 문장이 input으로 주어졌다고 가정해보자.
만약 RNN이라면 다음과 같은 플로우로 state가 갱신된다.
- “I love” → hidden state h1
- (h1, “you”) → h2
- (h2, “so”) → h3
- (h3, “much”) → h4
반면 Attention은 다음과 같다.
- (I love you so much) x (I love you so much)
이 둘의 의미론적 차이는 RNN은 이전 단어(토큰)을 사람처럼 시퀀스로 읽어내린다는 거다. 위에서의 Attention은 통으로 보기 때문에 I love you so much인지 you love so I much 인지 알바가 아니다. (I, love), (I, so) .... 토큰과 토큰사이 관계를 행렬곱연산 할거기 때문이다.
그렇기 때문에 Attention에는 'Positional Embedding'이 필요하다. 이 'I' 가 문장 앞에 있는지 어디에 위치한지 추가적인 정보를 주입해주는 것이다.
1. PE (Positional Embedding)
positional embedding은 token의 위치를 임베딩화 한 것이다. Attention is all you need 논문에서 제시한 PE 식은 다음과 같다.
각 dim마다 (2i, 2i+1) 짝수는 sin, 홀수는 cos를 사용해서 위치를 표시하는 것이다. 이는 퓨리에 변환으로도 이해할 수 있는데, 지금은 다루지 않겠다. 결국 PE의 목적은 토큰에게 위치값을 부여하기 위함이다.

토큰이 0번째 위치라면 PE(0, 2i) = sin(0) == 1 , PE(0, 2i+1) = cos(0) == 0
1번째 위치라면 PE(1, 2i) = sin(1 / 10000**(2i/d)) == 1 , PE(1, 2i+1) = cos(1 / 10000**(2i/d)) ....
식으로 전개될 것이다.
모델에서 input tokens가 주어졌을 때 1) 토큰을 embedding하고 2)토큰의 위치도 embedding해서 이를 더한다. concat이 아니라 더하기다. 다음과 같은 예시로 이해해보자.
- input: '나는 사과를 좋아해', vocab_sizse: 30522, hidden state size(위에서의 d에 해당함) : 512
- input 토크나이징을 했더니 5개가 나왔다고 가정. '나', '##는', '사과', '##를', '좋아해'
- token embedding 1
- embedding input shape: (5, 30522)
- embedding weight shape: (30522, 512)
- -> embedding 결과 shape (5, 512)
- token embedding 2(PE)
- positional embedding input shape: (5, 512)
- ~= token embedding 1의 결과
- positional embedding 결과 shape: (5, 512)
- ~= cos, sin 변환한 결과
- positional embedding input shape: (5, 512)
- embedding1 + embedding2 결과 shape: (5,512) + (5,512) == (5, 512)
이후 계산된 Token Embedding을 기준으로 attention Q(query) K(key) 연산을 수행한다.
참고로, PE도 위 수식을 그대로 적용하는 것이 아닌 learnable parameter로 생각해서 학습하는 방법론들도 여럿 나왔다.
2. RoPE (Rotary Positional Embedding)
Qwen3 등 오픈된 모델 아키텍처를 보면 PE는 거의 RoPE를 사용하는 추세다. PE에서는 한 토큰에게 위치에 해당하는 값이 임베딩으로 주어졌다면, RoPE에서는 토큰 간의 상대적인 위치를 본다는 차이가 있다. 상대적인 위치를 '회전'의 개념으로 본다.
θ 각도만큼 2x2 dim 행렬을 회전시키기 위해서 대학 수학수업에 배운 걸 상기시켜 보자.
(cos -sin
sin cos)
위 행렬을 원 행렬 A와 행렬곱을 하면 A를 θ 만큼 회전시킨 결과가 나온다. 이때의 θ는 아래 수식과 같다. PE에서 본 것과 유사하다.

다시 돌아와서, 0번째와 n번째에 위치한 토큰간의 어텐션을 구하고 싶다면 어떻게 해야 할까? 이 두 토큰의 위치간 차이를 θ로 생각해서 회전시킨 후에 둘의 내적(임베딩간의 유사도)값을 구한다. 그러면 두 토큰이 얼마만큼 상대적으로 떨어져 있는지를 알 수 있다.
그래서 RoPE에선 Q, K weight를 적용한 상태에서 rotation을 시킨다. 현재 벡터가 얼마나 상대적으로 거리감이 있는지 계산하기 위함이다.
정리해보자면 RoPE는 다음과 같은 흐름으로 계산된다.
- 다시 등장한 input: '나는 사과를 좋아해', vocab_sizse: 30522, hidden state size(위에서의 d에 해당함) : 512
- input 토크나이징을 했더니 5개가 나왔다고 가정. '나', '##는', '사과', '##를', '좋아해'
- 여기서 '나' 와 '##를' 간 상대거리를 RoPE를 통해 구해보자.
- 이때 token embedding shape (5, 512)
- '나', '##를' token embedding을 했다고 하자.
- 여기서 query, key에 대한 weight를 곱해준다.
- '나' 행렬 -> weight곱 해서 행렬 A로 정의.
- '##를' 행렬 -> weight곱 해서 행렬 B로 정의.
- RoPE
- 0번째 토큰(여기선 '나')의 A를 θ(여기선 0)만큼 회전변환함. -> R_a
- 4번째 토큰('##를')의 임베딩 B를 θ'(~= 10000*(-2i/d))만큼 회전변환함. -> R_b
- -> np.dot(R_a, R_b) 를 함으로써 A와 B 간 상대적 거리를 포함한 값을 구했다.
3. PE vs RoPE
PE와 RoPE를 적용한 token embedding을 시각화하면 다음과 같다.
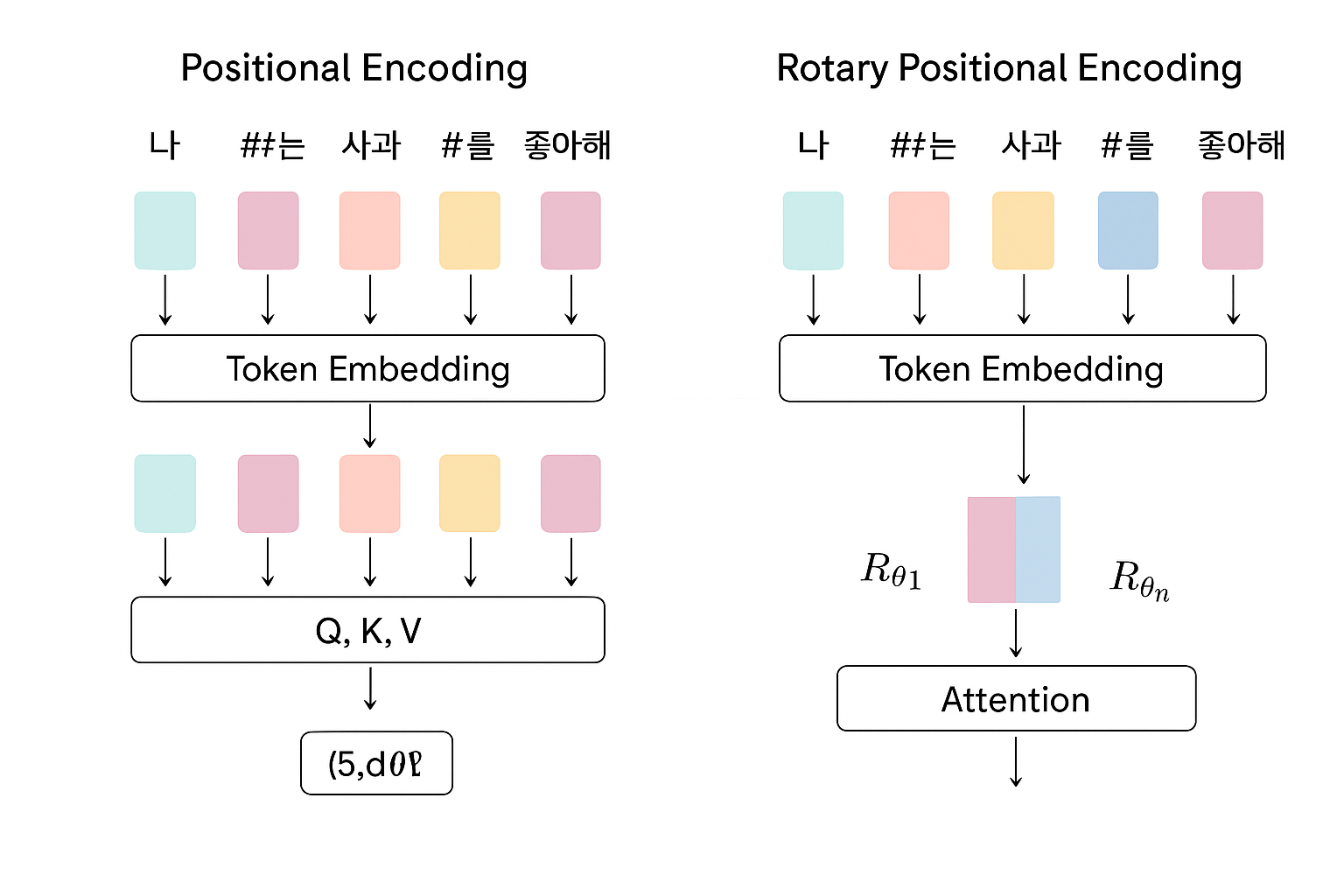
PE가 1) token embedding(token embedding + positional embedding) 후 2) Q, K에 대한 attention을 구한다면,
RoPE에선 1) token embedding의 과정에서 Q, K 값을 구해 2) rotation을 시켜 내적을 해 attention을 구하는 것이다.
'머신러닝 > 기초 머신러닝' 카테고리의 다른 글
| 딥러닝 모델 GPU 메모리 계산하기 (0) | 2025.09.21 |
|---|---|
| Spark Client vs Cluster mode 차이 (0) | 2025.09.07 |
| transformer의 모든 것 (0) | 2024.04.28 |
| Attention 기초 수식 설명 (0) | 2023.12.17 |
| PCA의 완벽한 이론 설명 (0) | 2023.10.29 |