오늘은 factor analysis, 차원 축소 기법으로 잘 알려져 있는 PCA에 대해 다룰 예정이다. 데이터를 특정 차원으로 매핑하여 임베딩을 하는 방법론과 유사하게 생각할 수 있다. 데이터 시각화에서 자주 쓰이는 분야인데, SVM에서 데이터의 eigenvector 분리를 통해 이미지 압축 등을 했던 것이나 Fisher LDA에서 데이터를 projection했던 거를 연상할 수 있다.
이 방법론들과 PCA의 유사함과 다름을 수식을 통해서 이해해보자.

주의 : PCA가 무엇인지 어렴풋이 아는 상태에서 보는 걸 추천함.
참고 : 머피의 머신러닝 1 20장
1. PCA란
Principal Component Analysis(PCA)는 이름을 직역하면 주성분분석이다. 데이터 x가 있다고 할 때, 이 x의 주 성분인 벡터들만 남겨서 x의 차원을 줄여버리는 것이다. 이때 x를 사영하고자 하는 공간을 z라고 하면 다음과 같이 W라는 벡터를 통해 x와 z의 관계를 정의할 수 있다.

- z = trans(W) x : x의 encoding 결과값인 z.
- x^ = Wz : z를 decoding하여 x로 복원한 값.
이렇듯 1. (x를 encoding한 z)를 2.(decoding하여 x로 복원한 값)인 x^와 x를 비교했을 때 둘의 차이가 최대한 적어야 좋은 w를 골랐구나 생각할 수 있다. 이를 reconstruction error, 또는 distortion이라고 한다.

L을 minimize하는 최적의 W는 x의 eigenvector와 연관이 있는데 , 지금부터 천천히 수식을 따라 설명해 보겠다.
2. 최적의 latent vector Z 구하기
위의 1. PCA 설명을 통해 PCA는 x를 encoding한 z로 차원을 축소하는 것을 목표로 하고, 이를 위해 reconstruction error를 minimize하는 방향으로 z와 w를 찾음을 알게 되었다. z를 찾기 위해서는 x에 곱해지는 벡터 w를 찾아야 한다 ( z = trans(w) x ). 이 관점으로 reconstruction error 를 다시 작성해 보면 아래와 같다. x를 encoding한 행렬 Z에 다시 wT를 곱하면 decoding한 결과가 되기 때문이다.

결국 PCA에서 우리가 건드릴 수 있는 값은 w밖에 없다. 최적의 w는 데이터 x가 갖는 공분산의 eigenvector인데, 이제부터 왜 그렇게 되는지 증명해보도록 한다.
z가 하나일 때( = 주성분이 하나일 때)
x의 주성분이 하나일 때를 생각해보자. 이때는 N개의 데이터가 있을 때 reconstruction error를 다음과 같이 전개할 수 있다. PCA는 'w는 orthogonal한다'다는 가정을 전제하에 진행이 된다. orthogonal함은 W 내의 row들이 서로 직교한다는 뜻이며, 이는 i, j번째 row에 대해 wi wi = 1, wi wj = 0 을 의미한다. w1 w1 = 1임을 기억하자.

새로이 전개한 이 loss를 미분해서 0이 되는 지점을 찾아보자. 이때 미분은 z를 기준으로 한다.

loss에서 x가 zw와 유사할수록 값이 작아졌던 것과 같이 (x = zw) 미분 결과가 0이 될려면 z = trans(w1) x 일 때 에러값이 최저가 됨을 보였다. 여기서 구한 z = trans(w1) x를 다시 reconstruction loss 수식에 대입해 보자. 원본데이터 x의 평균이 0이라고 가정한다면 loss는 w와 ∑(x의 공분산) 로 정리할 수 있다.

여기서 w가 무한대로 커지는 것을 방지하기 위해 w의 크기가 1이라는 constraint를 추가해 보도록 한다. 이는 lagrange multiplier를 통해 이룰 수 있는데, 간단하게 설명하면 ||w|| = 1 임을 추가하기 위해 식에 (||w|| - 1) 의 값을 일정 값만큼(보통 람다로 표현한다) 더하거나 빼준다. (참고 : https://hi-lu.tistory.com/entry/%EC%95%84%EB%A7%9E%EB%8B%A4-Lagrange-Multiplier-%EC%9D%B4%EB%A1%A0-%EC%A0%95%EB%A6%AC)

이제 reconstruction loss를 우리 입맛대로 변형하는데 성공했다. 다시 loss의 미분값이 0이 되는 지점을 찾아보자.

재미있게도 w1은 ∑의 eigenvector 형태로 식이 정리되었다! (EVD에서 eigenvector를 설명할 때 어떤 행렬 A에 대해 AU = λU로 표현할 수 있으며, 이때의 U는 eigenvector, λ는 eigenvalue였다. 자세한 설명은 이전 글 중 https://hi-lu.tistory.com/entry/Eigenvalue-Decomposition-EVD%EC%9D%98-%EC%88%98%EC%8B%9D-%EA%B8%B0%EC%B4%88 참고.)
loss가 작을수록 좋으므로 λ값은 클수록 좋다. 따라서 최적의 w는 가장 큰 eigenvalue(λ)일 때의 eigenvector임을 알았다.
z가 여러개일 때 (= 주성분이 여러 개일 때)
주성분이 여러개일 때에도 최적의 w가 같은 조건을 가진다. 이를 증명하기 위해 Z가 2dim일 때의 reconstruction loss를 살펴보자.
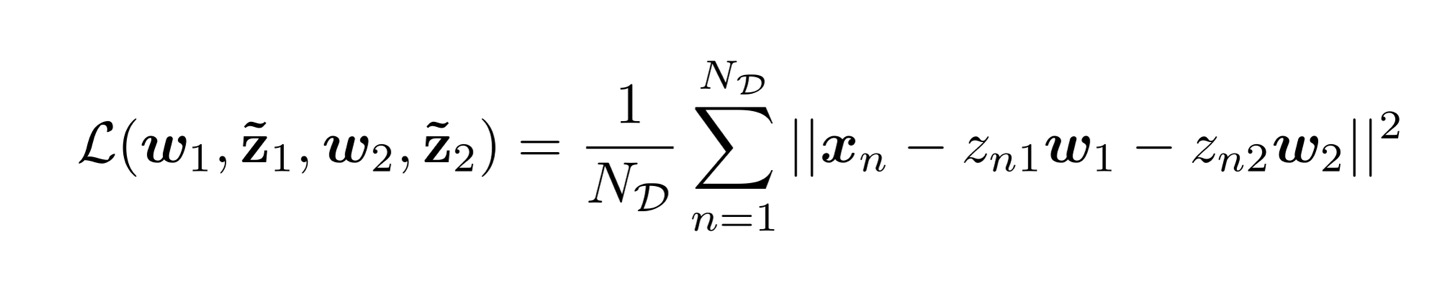
Z가 1dim일때와 동일하게 식을 전개해서 w에 관한 식으로 풀어내면 자연스럽게 w1이 사라진다. W가 orthogonal하기 때문에 w1w1 = 1, w1w2 = 0이기 때문이다.

동일하게 w의 크기를 1로 제한해서 loss를 변형해주자. 추가로 orthogonal한 특성인 w2 w1 = 0도 loss에 반영될 수 있도록 lagrange multiplier를 하나 더 추가해 주었다.
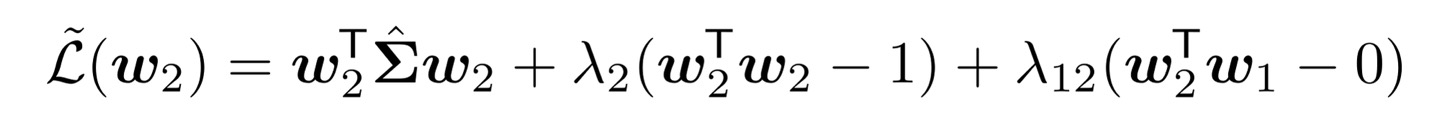
구한 loss를 w2에 대해 미분했을 때 0이 되는 식은 z의 dimension이 1일 때와 유사한 형태로 아래와 같이 나타난다. 즉, dimension이 2일 때에도 w2는 공분산의 eigenvector 형태다.

마지막으로 모든 dimension에 대한 w들이 이에 성립하는지 보기 위해, 일반화를 해보면 다음과 같이 x dim이 2일 때의 loss를 쭈욱 늘여 서 증명할 수 있다. (스킵해도 된다.)

따라서, pca에서 최적의 사영벡터 w는 x의 공분산의 eigenvector이며, 이때 벡터들은 eigenvalue가 큰 순으로 나타난다.
Z의 분산
다시 x의 차원이 1일 때로 돌아와보자. x의 평균이 0이고, w이 orthogonal할 때 최적의 w를 구해 최종적으로 구하고 싶은 목적인 z를 구할 수 있었다. 이번에는 z의 분산을 구해서 재밌는 사실을 발견해 보자.

위 식을 통해 z의 분산이 loss와 반비례한 것을 볼 수 있다. PCA를 돌려보면 주성분들은 주로 분산이 큰 방향으로 설정이 되는걸 확인할 수 있는데, 수식적으로도 z의 분산이 커지는 방향으로 임베딩이 되는 것을 알 수 있다.
아래 그림을 통해서도 z1의 주성분들에 따른 분산값을 확인할 수 있다. 오른쪽 figure의 첫번째 latent vector(z1의 1번째 주성분)과 두 번째, 세 번째의 분산이 갈수록 줄어듦을 확인할 수 있다.
3. Computational issue
왜 PCA 이전에 standard normalize 해줘야 할까
w를 구하기 위해 x의 covariation matrix를 이용함을 위에서 보였는데, 이때 correlation matrix를 이용하는게 더 좋다. (correlation(corr)는 covariance(cov)를 분산으로 normalize 한 버전이다. ) 앞에서 언급했다시피 latent vector z(=wx)는 분산이 큰 방향으로 이동하기 때문에, 분산을 normalize해준 것과 그렇지 않을 때의 pca 결과가 다르게 나온다.
그래서 보통 pca를 넣기 전에 scaler를 통해 x를 standarization 한 후(분산으로 나눠서 x를 standard하게 해 주기.) pca를 계산하고는 한다. 게다가 이미 계산 시에 x이 centered 되었다고 가정했기 때문에(x의 평균이 0), sklearn의 standard scaler를 적용해 주면 평균도 0으로 맞추고, 분산도 normalize 해줄 수 있다.
SVD 이용하기
PCA의 w를 구하기 위해서는 x의 공분산(covariance matrix)의 eigen decomposition을 계산해야 하는데 원 데이터 x의 차원이 높을수록 이를 계산하는데 드는 cost가 커지게 된다. 어차피 x의 공분산을 구하는 거니, truncated SVD를 통해 Z를 구하는 것이 가능하다. SVD를 간단하게 설명하면 X = U λ trans(V) 로 나타낼 수 있는데 이때 U는 Xtrans(X)의 eigenvector, V는 trans(X)X의 eigenvector다.(이전글 참고 : https://hi-lu.tistory.com/entry/SVD-Singular-Value-Decomposition-%EC%88%98%EC%8B%9D%EC%A0%81-%EC%9D%B4%ED%95%B4 )
지금부터 이 특성을 이용해서 X를 decomposition 하며 Z를 자연스럽게 구해볼거다. X의 공분산을 trans(X) X 로 표현가능한데(우리가 이미 X의 평균이 0이라고 가정했기 때문에) 이 공분산의 eigendecomposition을 eigenvalue가 큰 순서대로 L개를 사용해서 해보자.
- trans(X)X ~= USV (이때 U는 left singular, V는 right singular vector)
- W는 X의 공분산의 eigenvector
- X의 공분산 = trans(X) X
- W = V
이 특성들을 기억하며 Z = WX에 대입해 보자.

X를 decomposition하니 자연스럽게 Z를 구할 수 있게 되었다. decoding한 X^도 아래와 같이 구할 수 있다. X^가 돌고 돌아 다시 X의 turncated SVD 형태와 동일해졌음을 알 수 있다.
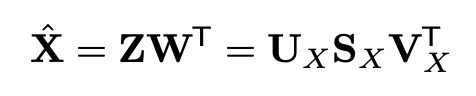
따라서 X를 decomposition하는 것은 PCA에서 L번째까지의 주성분을 구하는 것과 마찬가지가 된다. 이는 공분산인 Xtrans(X)를 decomposition 하는 것보다 연산량이 적은 편이라 좋은 선택지가 될 수 있다.
4. 몇개의 주성분 벡터까지
reconstruction error plot
X가 n개의 dimension으로 이루어져 있어 Z도 n개의 row를 가진다고 하자. 대개 PCA를 사용하는 이유는 x를 차원축소하여 피쳐를 추출하고자 함인데, 모든 n개의 피쳐(n dim)를 다 쓰기위해 pca를 사용하진 않을 것이다. 몇 개까지의 피쳐 z를 고를 것인지 선택하기 위해서는 error를 plot 형태로 그려 몇 개까지의 principal component일 때까지 가장 급격하게 loss가 줄어드는지 체크해 볼 수 있다. (어차피 n개 다 쓸 때가 loss는 제일 적을 것이다.)
scree plot
또다른 방법으로는 scree plot을 그려보는 것이다. 위에서 최적의 w는 x 공분산의 eigenvalue가 큰 순으로 가지는 eigenvector임을 보였었다. screet plot은 eigenvalue에 해당하는 λ에 대한 plot을 그려보는 형태인데, 채택하는 피쳐 dim 이 커질수록 해당 w와 짝지어지는 eigenvalue (λ) 값은 당연하게도 작아질 것이다. scree plot을 통해 λ이 급격하게 작아지는 부분을 확인하고, 적절하게 latent dimension을 고를 수 있을 것이다.

profile likelihood
마지막으로 profile likelihood를 확인해 볼 수 있다. 이는 n개의 latent vector(주성분)들이 있을 때 어떤 k를 통해 k번째 이전 주성분들과 대응하는 eigenvalue의 합과 k번째 이후 주성분들과 대응하는 eigenvalue의 합을 비교해 보는 것이다. 그러면 plot은 어느 순간 피크를 찍고 내려오는데, 피크에 해당하는 k번째 주성분들이 가장 의미 있는 정보들을 담아내고 있다고 해석할 수 있다.
오늘은 PCA를 계산하는 방법에 대해 중점적으로 알아보았고, 이를 통해 몇번째 주성분까지 선택하면 좋을지 관찰하는 법도 정리해 보았다.
'머신러닝 > 기초 머신러닝' 카테고리의 다른 글
| transformer의 모든 것 (0) | 2024.04.28 |
|---|---|
| Attention 기초 수식 설명 (0) | 2023.12.17 |
| Mutual Information 파헤치기 (0) | 2023.10.14 |
| 엔트로피와 KL Divergence (0) | 2023.10.08 |
| linear regression의 완벽한 기초 수식 (0) | 2023.09.30 |