오늘은 지난 글 EVD에 이어서 SVD에 대해 정리해 본다. 이번 글은 머피의 머신러닝 1의 7.5장에 근거한다.
0. 들어가면서
EVD 요약
Eigenvalue Decomposition은 행렬 A에 대해 eigenvalue(Λ)와 eigenvector(U)로 다음과 같이 표현할 수 있었다.
AU = UΛ
만약 여기서 A가 대칭행렬일 경우 U가 orthogonal(직교) 행렬이기 때문에 U의 역행렬이 U의 전치행렬과 같았다. 따라서 A를 아래와 같이 표현할 수 있었다. 참고로 orthogonal행렬은 각 컬럼이 서로 직교하기 하는 행렬이다. 만약 이 컬럼들이 normalization도 만족한다면 (컬럼의 크기가 1) 이 행렬은 orthonormal하다.
A = UΛ trans(U)
Eigenvalue Decomposition (EVD)의 수식 기초
오늘은 Eigenvalue Decomposition(EVD)에 대해 빠삭하게 정리해보고자 한다. Singular Value Decomposition(SVD)를 설명하기 전 사전지식을 한 글로 떼어내서 다뤄볼 것이다. 본 내용은 '머피의 머신러닝 1'의 7.4장
hi-lu.tistory.com
pseudo inverse
역행렬을 구할 수 없는 행렬의 경우엔 EVD와 같은 행렬 분해 연산이 힘들 것이다. 이럴땐 pseudo inverse를 통해 임의로 행렬 A의 역행렬을 지정할 수 있다. 아래 4가지 조건을 만족하는, 기호로 십자가 표기가 붙어있는 행렬이 이에 해당한다.

1. SVD
어떠한 행렬 A(m*n행렬) 에 대한 SVD를 수식을 보면 EVD와 유사한 생김새인걸 알 수 있다. 아래 수식에서 왼쪽의 U(m*m)와 오른쪽 V(n*n)는 orthonormal한 행렬로 각각 left sigular vector, right singular vector라고 부른다. 가운데의 S(m*n)는 singular value(특이값)로 채워진 대각행렬을 의미한다. 두 번째 수식 상 σ가 이에 해당한다. 각 uvT에 대해 σ 만큼의 가중치를 주고 있는 셈이다.
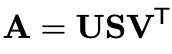

SVD로 행렬 분해한 결과를 그림으로 나타내면 두가지로 나타낼 수 있다. 아래 그림들에서 m*n 짜리 행렬 A에서 m > n일 때와 m <n일 때 A가 U, S, V 행렬로 어떻게 분해되는지 볼 수 있다. 이때 행렬들의 크기 자체가 변하진 않지만 원 행렬 A의 크기에 따라 파란색 부분을 0으로 padding 해주고 있다.

SVD와 EVD
만약 행렬 A가 실수에 대칭행렬이고 모든 성분이 0보다 크다면, A의 singular value(S)는 eigenvalue와 같으며 singular vector(U, V)는 eigenvector와 같다. 즉 이때 특이값은 고유값과 같고 특이벡터는 고유벡터인 것이다. 이러면 A의 SVD는 EVD 수식과 완전히 동일해진다. 이 말은 즉 EVD가 SVD의 special case가 되는 셈이다.
이번엔 행렬 A가 임의의 실수로 이루어져 있다고 가정하고, A*trans(A)와 trans(A)*A를 구해보자. 먼저 A*trans(A)다.

A*trans(A)가 위와 같이 정리되었다. 이때 우변의 trans(U)를 좌변으로 옮긴다면 Atrans(A)의 EVD가 된다. (EVD의 정의를 기억하자.)

두 번째로 trans(A)*A에 대해서도 구해보자.

마찬가지로 trans(V)를 좌변으로 옮긴다면 trans(A)A의 EVD가 된다.
이를 종합해보자면 U는 Atrans(A)의 eigenvector, V는 trans(A) A의 eigenvector, D는 eigenvalue인 것이다!
pseudo inverse using SVD
행렬 A가 non singular라 역행렬을 없다고 가정하자. A의 역행렬을 구하기 위해선 pseudo inverse를 구해야만 하는데, 이때 SVD로 구할 수 있다. trans(A)가 full rank고 A가 선형독립이라면 A의 pseudo inverse는 아래와 같은 식을 만족한다. 이 식에 A = UStrans(V)를 대입해 보자.
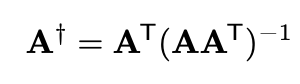

오, SVD를 통해 A의 pseudo inverse를 구해보았다!
Truncated SVD
SVD를 통한 특이분해를 진행했을 때 첫 K개 컬럼에 대해서만 말하고 싶다면 Ak = Uk Sk trans(Vk)로 나타낼 수 있다. 이 K값을 최적으로 가져가고 싶다면 A와 Ak간의 차이를 minimize하는 식을 통해 k개 특이분해 column만 가지고 행렬 압축 등이 가능하다.

만약 A의 rank(==r)가 k와 같다면 A와 Ak는 사실상 같을 것이다. (A의 rank는 singular value 수와 같다는 사실을 기억하자.) 여기서 A를 더 압축하고 싶다면 이때를 truncated SVD라고 부른다. k < r인 k개의 특이값들을 사용한다는 것이다. 재밌는 점은 A와 Ak의 차가 k+1 ~ r번째 singular value 합과 같다. (U, V가 orthonormal이었던걸 기억하자.)

오늘은 지난번부터 밑밥을 깔아왔던 SVD에 대해 정리해 보았다. singular value 중 가장 큰 값이 보통 1번째로 위치하게 되는데, 그래서 SVD의 적은 수의 rank만 가지고(특이값들의 top k개만 쓰는 등) 특이값들을 조합해서 영상 압축 등에 쓰일 수 있다. 본 글을 통해 SVD와 EVD의 전반적인 수식적 이해를 도왔기를 바란다.
'머신러닝 > 아맞다' 카테고리의 다른 글
| 엔트로피와 KL Divergence (0) | 2023.10.08 |
|---|---|
| linear regression의 완벽한 기초 수식 (0) | 2023.09.30 |
| Eigenvalue Decomposition (EVD)의 수식 기초 (0) | 2023.09.16 |
| GMM과 EM의 완벽한 이해 (0) | 2023.09.09 |
| 머신러닝 앙상블 기초, bagging, boosting, stacking, random forest 기법 (0) | 2023.08.26 |