지난 포스트에서는 MAB와 Epsilon Greedy, Thompson Sampling에 대해서 정리했다. 이번에는 조금 더 진도를 나가서 LinUCB에 대해 알아보자.
0. 사전 지식
Contextual Bandit
강화학습과 추천에서 Bandit은 어떤 것을 선택해야 최적의 값이 나올까를 고민한다. MAB(Multi Armed Bandit)는 여러가지 선택지 (arm. 또는 action)에서 최적의 reward를 가지는 것을 선택해야 한다.
contextual bandit은 MAB에서 context(상황)을 추가로 고려한다. 현재의 상황에 대한 피쳐가 있다고 가정했을 때(x_t), 이를 기반으로 action(a)을 선택하게 된다.
- P(a | x_t)
MAB에서 모든 상황을 동일하게 가정하고 최적의 reward를 고르는 것과는 다르다.
1. LinUCB
Lin
기존의 MAB에서 action이 가지는 reward 기댓값이 θ 였다면, context를 고려하기 시작하면 '해당 컨텍스트에서 action을 취할 확률'을 구해야 한다.
이를 선형적(linear)으로 결합한다면 θ * x 으로 볼 수 있다. θ가 arm을 선택하기 위한 weight이 된다.
| before | after |
| rₜ(a) = θₐ + ϵₜ | rₜ(a) = θₐ*x + ϵₜ |
UCB
UCB는 Upper Confidence Boundary를 뜻한다. 추천에서 exploration(탐험)과 exploitation의 적절한 균형을 찾는 일은 계속되어야 한다. 특정 arm(action)에 대해서 생각해보자.
이 arm을 선택할 때 exploration의 관점은 일종의 불확실성이다.
반면 exploitation은 이 선택을 함으로써 받게 될 reward(μ)를 계산할 수 있다. 이는 평균 reward로 이해할 수 있다.
특정 arm을 선택했는데 exploration으로 선택했든, exploitation으로 선택했든, 둘 다의 관점에서 얻을 수 있는 점수의 최대치(upper bound) 는 다음과 같이 UCB 수식으로 설계할 수 있다. 즉 이는 이 arm을 선택했을 때의 최대 reward 추정치다.
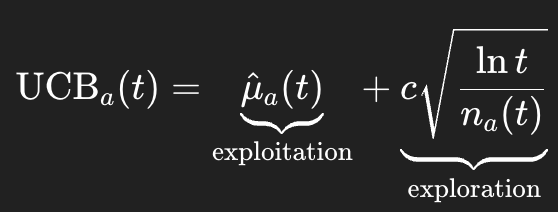
위 수식에서 t는 시간, n_a(t)는 지금까지 이 arm을 선택한 횟수를 의미한다. exploration 항은 즉 arm을 선택한 적이 없을수록 커진다.
LinUCB에서의 UCB
UCB 점수는 다음과 같이 정의된다.

1) exploitation reward μ는 context x를 고려했을 때 선형적으로 θ * x 로 표현할 수 있었다.
- θ_a ⊤ x_t
2) exploration항은 해당 arm을 얼마나 많이 선택했었냐에 대한 항이었다. 이를 context x와 arm을 선택했던 컨텍스트들 x_t의 선택 유무 행렬 A를 활용해 정의할 수 있다.

이때 A는 design matrix이다. 시점 s에 action a를 선택한 컨텍스트 피쳐 x에 대한 정보가 담겨있을 것이다.
- = 시점 s에서 arm a가 선택되었을 때의 컨텍스트(feature) 벡터
x_s를 outer product 한걸 summation한 것은 피처별로 covariance를 포함한 상호관계를 더했다고 해석할 수 있다. 이 더한 값에 I를 더함으로써 cov 행렬을 완성했다.

A의 역행렬은 공분산의 역수이기 때문에, t 시점의 정보들이 많다면 작은값을 나타낼 것이다. 여기에 현 컨텍스트 x_t를 곱한다면, x_t가 지금까지 action을 선택했던 feature중에서 얼마나 낯선 것인지 점수화할 수 있다.
예시
예를 들어 현재 컨텍스트 피쳐가 2개라고 해보자. arm1을 선택했던 컨텍스트는 지금까지 총 2개 있었다고도 해보자.
- x_1 = [1 ; 2] (1x2dim)
- x_2 = [0; 1] (1x2dim)
그럼 A_1 = x_1 x_1_t + x_2 x_2_t + I 이므로
[1;2] [1;2]T + [0;1] [0;1]T + I
[1 2 + [0 0 + [1 0 == [2 2
2 4] 0 1] 0 1] 2 6]
이다. 즉, A_1 == [2 2 ; 2 6] (2x2 dim)
이의 역행렬을 계산한다면 [0.75−0.25 ; −0.25 0.25] (2x2dim)이다.
여기에 현재 t의 컨텍스트 x_t의 첫번째 피쳐는 1, 두번째 피쳐는 1이라고 해보자. x_t = [1 ; 1]
그럼 현 피쳐에서 arm1을 선택했을 때 exploration 점수는,
trans(x_t) * A_1 -1 * x_t 이므로
[1 1] * [0.75 -0.25 * [1
-0.25 0.25] 1]
== 0.5다.
물론 여기에 exploration 계수 α를 곱해줘야 한다.
그러면 현재 arm 1 의 UCB점수는 다음과 같이 구해진다.
- UCB_a1 = trans(θ_a1) *[1;1] + α * 0.5
여러 arm 중에서 UCB값이 가장 높은 arm을 선택하게 될 것이다. 선택한 arm의 reward에 따라서 현시점 t에서의 디자인 벡터 A도 업데이트되고, 예상 reward θ도 업데이트된다. (이때 θ는 linear regression으로 업데이트된다.)
'머신러닝 > 기초 머신러닝' 카테고리의 다른 글
| 추천시스템 Matrix Factorization (MF) 와 ALS (0) | 2025.10.31 |
|---|---|
| 딥러닝 모델 GPU 메모리 계산하기 (0) | 2025.09.21 |
| Spark Client vs Cluster mode 차이 (0) | 2025.09.07 |
| Positional Encoding 과 RoPE에 대하여 (0) | 2025.08.30 |
| transformer의 모든 것 (0) | 2024.04.28 |