오늘은 Matrix Factorization(MF)와 Alternating Least Square(ALS)에 대해서 알아보고자 한다.
참고: [paper] Collaborative Filtering for Implicit Feedback Datasets
0. 선수 지식
SVD
Singular Value Decomposition(SVD)에 대해선 이전 포스트에서 자세히 다룬 적 있다.
SVD (Singular Value Decomposition) 수식적 이해
오늘은 지난 글 EVD에 이어서 SVD에 대해 정리해 본다. 이번 글은 머피의 머신러닝 1의 7.5장에 근거한다. 0. 들어가면서 EVD 요약 Eigenvalue Decomposition은 행렬 A에 대해 eigenvalue(Λ)와 eigenvector(U)로 다음
hi-lu.tistory.com
간략하게 정리해보면 SVD란 하나의 행렬을 고유행렬들로 분해하는 과정이다. A라는 행렬이 주어졌을 때 두개의 singular 행렬(U, V)과 특이값의 대각행렬(S) 곱 형태로 나타낼 수 있다. 이때 A가 대칭행렬이라면 분해된 singular 행렬은 eigen vector, eigen value와 같다.
A = U S trans(V)
1. Matrix Factorization
유저와 아이템 메트릭스가 있다고 가정해보자. 유저가 아이템과 인터렉션 한 값이 행렬로 채워진 상태, 예를 들어 유저수 1000만, 아이템 수 1만이라고 해보자. 유저-아이템 메트릭 A의 shape는 (10,000,000 , 10,000) 이 된다. 벌써 연산값이 어마어마하다.
이를 SVD를 적용해서 특이값행렬 U, V로 짜개볼거다. U의 shape는 (10,000,000, r) V는 (10,000, r) 이다. r은 그럼 잠재적인 factor가 되는데, 벡터 U의 입장에서는 행렬 A에 대한 left singular vector이기 때문에 유저 row 별 임베딩으로 볼 수 있다.
r이 의미하는 것은 결국 latent factor로, 상위 r개 rank에 대한 피쳐를 남겨둔 것이다.
A = U S trans(V) 였다. 그러므로 다음과 같이 쪼갤 수 있다.

빨간색 1번이 유저 임베딩, 빨간색 2번이 아이템 임베딩으로 이해할 수 있다. 여기서 대각행렬 S은 각 r 열들의 importance 가중치를 의미하기 때문에, 상대적인 유사도를 구할 때 스킵해도 되는 요소가 된다.
따라서, np.dot(U, trans(V)) ~= 유저들의 아이템들에 대한 유사도가 될 수 있다. 1000만 by 1만 행렬연산을 안해도 되고, sparse vector에서 rank r로 압축되었기 때문에 표현력도 좋다.
Matrix Factorization(MF)의 행렬분해를 통해 유저-아이템 유사도를 구할 수 있음을 보았다.
2. MF와 ALS
그러나 SVD를 사용하기 위해서는 어쨌든 행렬 A가 어느정도 값이 채워져 있어야 한다. 죄다 null이면 애초에 특이값을 분해하기 힘들테니 말이다. 1000만 유저와 1만 아이템에 대한 interaction을 행렬로 나타냈을 때 만약 1만 아이템이 대부분 cold item이라면 어떻게 할까?
sparse metrix가 된다.
SVD를 통한 MF에서 우리는 행렬 A를 U, S, V로 나타냈으며, U는 유저임베딩, V는 아이템 임베딩으로 이해할 수 있었다. 이때 우리가 추천에서 알고 싶은 유저와 아이템 간의 유사도는 U*V로 나타낼 수 있음을 알았다.
이제 우린 ALS를 통해 sparse metrix A를 U와 V로 나타낸다. 이제 편의상 svd left singular vector였던 U는 P, svd의 right singular vector였던 V는 Q로 표현하겠다.
유사도 ~= np.dot(P , trans(Q))
P와 Q를 알게 된다면 SVD에서처럼 유사도를 구할 수 있게 된다. 그럼 어떻게 P와 Q를 구할까? ALS에선 P를 고정한 후 Q를 업데이트하고, Q를 고정한 후 P를 업데이트하는 형식으로 P와 Q의 최적값을 찾는다. 그래서 이름이 Alternating Least Square다.
A를 표현하는 것을 P와 Q 2개의 벡터로 하고자 한다. 따라서 objective function은 A와 P dot Q의 차를 loss term으로 둘 수 있다. 이는 선형회귀에서 잔차의 제곱을 최소화하고자 하는 Least Square와 유사하다. 식을 보니까 L2 loss와 유사하다. 그래서 이름이 Alternating Least Square 인가보다.
아래 식에서 r이 A, x와 y는 각각 P와 Q라고 볼 수 있다. 람다 항은 regularization term이다.
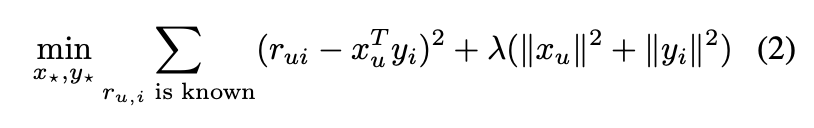
L2 loss는 다른말로 MSE loss다. 딥러닝에서 회귀 문제를 풀 때 목적함수로 주로 쓰는 형태다. 그말은 즉 이 object function을 minimize하는 일을 Gradient Descent(GD)로 풀수도 있다는 말이다.
하지만 우리는 ALS를 본다. row별 업데이트가 가능하기 때문에 대규모 데이터를 다룰 때 필요한 분산처리가 가능하기 때문이다.
위 term을 우리가 보기에 편하게 다시 써보면,
minimize (A - np.dot(P, trans(Q))**2 + lambda (||P**2|| + ||Q**2||)
ALS 컨셉 상 P를 계산할 때 Q는 상수취급을 받고, Q를 계산할 땐 P가 상수취급을 받는다. 따라서 P를 계산할 때는 Q 업데이트를 신경쓰지 않고 배치 업데이트가 가능할테고, 반대의 경우도 마찬가지다.
ALS의 spark 라이브러리 함수는 다음과 같다.
from pyspark.ml.recommendation import ALS
als = ALS(rank=10, seed=0) #rank ~= r을 의미한다. 상위 r개 피쳐까지로 압축할 것인가.
als.setMaxIter(5) #몇번 학습할건지
model = als.fit(df)
'머신러닝 > 기초 머신러닝' 카테고리의 다른 글
| 추천시스템 LinUCB 개념 파헤치기 (2) | 2025.10.11 |
|---|---|
| 딥러닝 모델 GPU 메모리 계산하기 (0) | 2025.09.21 |
| Spark Client vs Cluster mode 차이 (0) | 2025.09.07 |
| Positional Encoding 과 RoPE에 대하여 (0) | 2025.08.30 |
| transformer의 모든 것 (0) | 2024.04.28 |