오늘은 머피의 머신러닝 16.1장에 해당하는 KNN(K Nearest Neighbor) classifier에 대해 정리해 본다.
참고 : 머피의 머신러닝 1
들어가면서
nonparametric model
KNN은 CNN, RNN과 같은 딥러닝 모델과(parametric model)과 다르게 nonparametric model에 해당한다. parametic model은 데이터가 특정 distribution에 있기를 전제로 하고 학습을 진행한다면 nonparametric model은 그렇지 않다. 데이터가 특정 분포를 따른다는 전제 없이 모델을 학습한다.
parametric model들을 정의할 때 class posterior가 다음과 같이 표현되고는 했다. 이때의 θ가 데이터의 분포를 학습하고자 하는 파라미터를 의미하게 된다.
- p(y|θ) : unconditional
- p(y|x,θ) : conditional
반면 nonparametric model은 θ가 아닌 데이터(D) 자체에서 모델을 형상하게 되는데, 주로 거리함수(distance metric)등을 통해 input 데이터가 학습한 데이터들 중 누구와 유사한가를 찾는 방식이다. nonparametric model에는 KNN외에도 Tree계열 모델, Random Forest, Boosting 계열 등이 속한다.
KNN
이름에서도 알 수 있다시피 K개의 인접(nearest) 이웃(neighbor)을 토대로 결과를 예측하는 모델이다. 새로운 데이터 x (test input x)가 들어왔다고 가정했을 때, 학습 데이터 중 x와 유사한 K개의 데이터를 살펴보는 것이다. 그렇기 때문에 KNN 모델을 활용하기 위해선 학습한 데이터들이 저장되어 있고, 학습 데이터들이 어떤 공간에 특정 거리를 유지하며 분포되어 있을 것이다. 이 과정은 다음과 같이 진행된다.
- 분류하고자 하는 데이터 x가 들어왔다.
- 모델 학습 데이터 중 x와 가장 가까운 K개의 데이터를 뽑는다.
- K개 데이터의 라벨을 살펴본다.
- x 주변 데이터의 distribution을 알게 되었다.
아래 그림은 k값이 5일 때 새로운 데이터 x와 인접한 5개의 데이터를 비교하는 그림이다. 5개 중 3개가 1로, 2개는 0으로 라벨링되어 있으니 추가 가중치가 없다면 x는 0.6이란 확률로 1로 분류될 것이다.
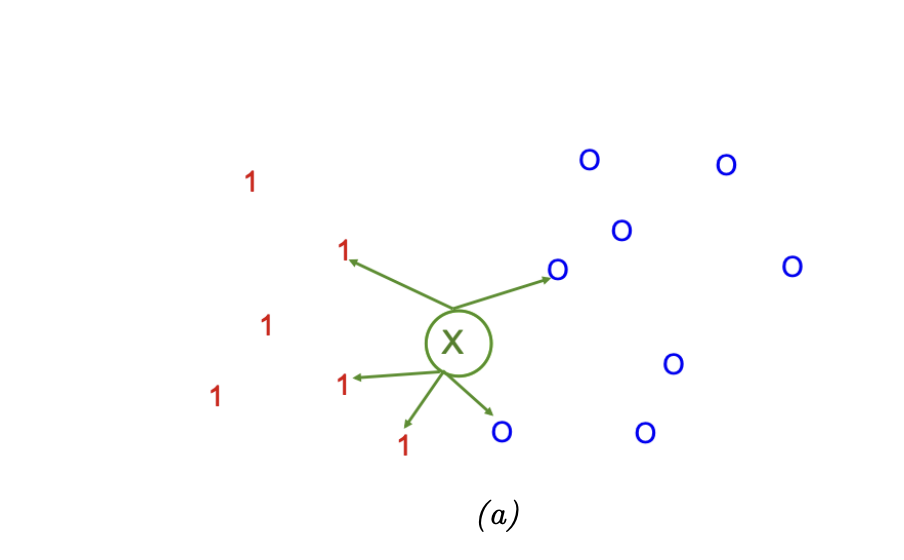
KNN의 수식은 class conditional 분포는 다음과 같다. 그림을 그대로 수식으로 옮겨놓은 것이다.

위 그림에 대입해서 생각해보면 다음과 같다.
p(y=1|x,D) = 1/5 * 3 = 3/5 ,
p(y=0|x,D) = 1/5 * 2 = 2/5
Mahalanobis distance
x와 가장 가까운 데이터 K개를 뽑기 위해서는 x와 학습 데이터 간의 거리를 측정해야 한다. KNN에서는 mahalanobis distance를 사용하는데, 이 함수는 다음과 같이 표현된다. x에 대해 정규화한 후 euclidean 거리를 구하는 수식이다.

추가 - 연산량 측면, 차원의 저주
연산량
KNN은 결국 학습한 데이터들을 저장해 놓고, 유사한 데이터들을 찾아서 연산해야 하기 때문에 연산량이 버거운 편이다. LSH(Locality Sensitive Hashing)이나 k-d tree를 사용하면 연산량을 줄일 수 있다. 파이썬 라이브러리 중 Faiss를 사용하면 KNN을 효율적이게 사용할 수 있다.
참고 : LSH에 대한 초간략 설명은 아래 접은 글에 있다.
LSH는 해싱 기법 중 하나로, 대용량 데이터를 분류하거나 검색하는 데 사용되는 알고리즘 중 하나다. 데이터를 해싱해서 비슷한 데이터가 같은 버켓에 담길 수 있도록 나눈다. 버켓에 들어간 데이터들은 유사하다고 생각하는 것이다. 100개의 데이터중 A와 비슷한 데이터를 찾는다고 가정해 보자. 100개의 데이터를 해싱해서 10개의 버켓에 담았다면 A는 100개가 아닌 10개의 해시값과 비교연산을 하면 된다. 그 후 유사한 해시값의 버켓을 찾았다면 해당 버켓 안의 데이터들은 A와 유사하다 볼 수 있다.
차원의 저주(curse of dimensionality)
데이터의 차원이 크다면 당연하게도 KNN은 잘 작동을 안할 것이다. 데이터의 차원 수가 크게 된다면 가장 가까운 이웃을 뽑아야 하는데 굉장히 멀리 있는 공간에서 찾아야 할 수도 있게 된다. 아래 그림은 차원의 저주를 설명한 그림이다. 그림 (a)에서는 데이터들이 D-dimensional unit cube 형태라고 가정했다. 큐브의 엣지 길이는 0~1 사이라고 가정한다. 데이터 x와 인접한 데이터를 구해야 하는데, 큐브가 커지면 커질수록 x 주변에 있던 라벨의 density는 점점 줄어들게 된다.
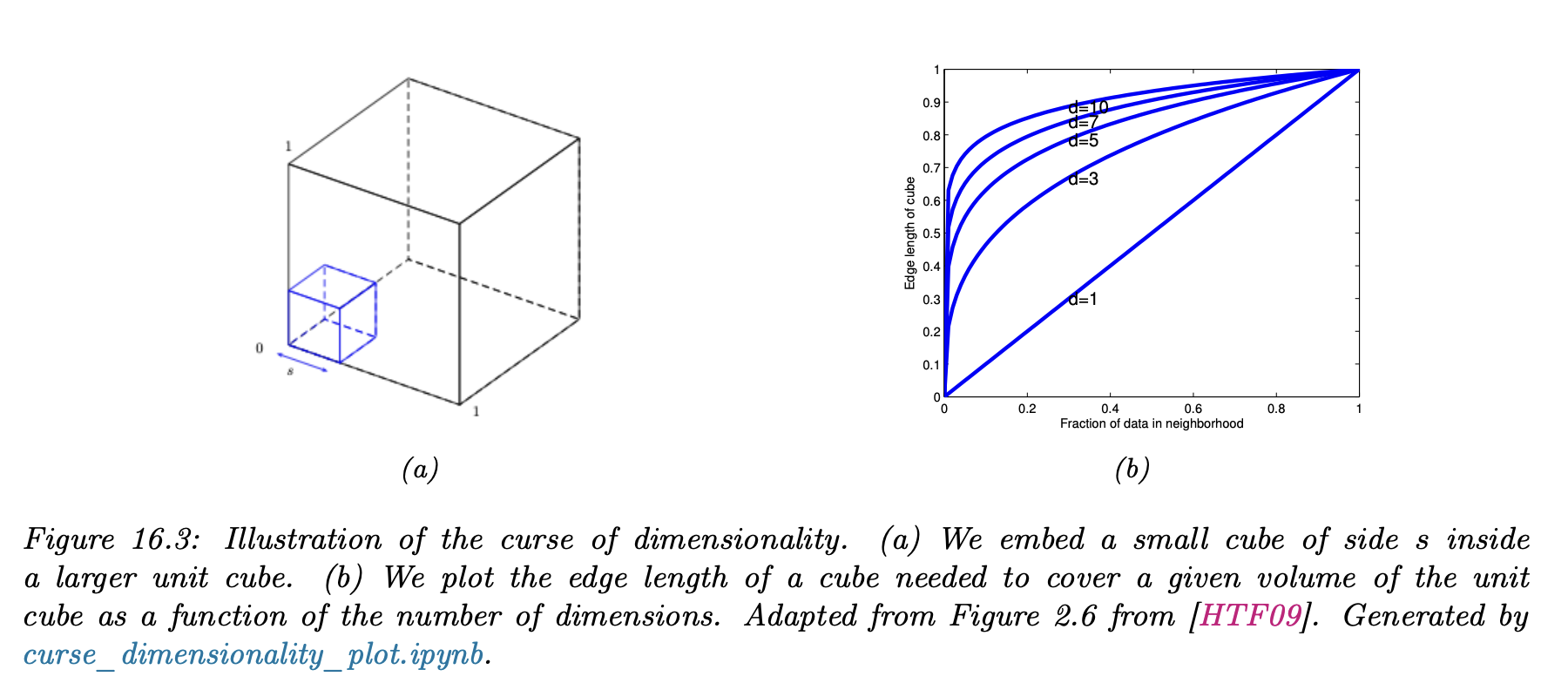
x 주변 데이터 수와 차원 수에 따라 탐색해야 할 공간의 크기를 어림잡을 수 있을까? 이걸 그래프한 것이 위의 그림 (b)이다. p개의 데이터를 봐야 한다면 이때 큐브의 edge 길이는 p의 수와 비례하고 차원 D의 크기와 반비례하다. 수식은 아래와 같이 나온다고 한다.

차원수가 10(D)이고, 10%(p)의 데이터만 보길 원한다면 edge 길이는 0.8이 나온다. 만약 차원수가 10이고 1%의 데이터만 본다 하더라도 엣지 길이는 0.63이 된다. 엣지 길이가 0~1 사이인데, 1%의 데이터를 보기 위해서 엣지 길이가 0.63 지점까지 데이터를 봐야 한다는 것은 '근처'를 보고 있다 할 수 있을까?
해결 방법은 두가지가 있다.
- parametric model을 일부 차용하기
- 일부 차원에 대해서만 계산하게끔 하기
책에서는 KNN의 사용 예 중 하나로 OOD(Out-Of-Distribution)나 face verification을 들었다. 실제로 metric learning 개념은 NCD(Novel Class Discovery)나 face recognition에서 사용되고 있다. 오늘은 KNN에 대해 정리해 보았지만, 개인적인 견해로 현업에서 자주 등장하는 편은 아닌 듯하다.
'머신러닝 > 기초 머신러닝' 카테고리의 다른 글
| Fisher LDA 이론 정리 (0) | 2023.08.20 |
|---|---|
| EM(Expectation-Maximization) 알고리즘의 완벽한 기초 (4) | 2023.08.13 |
| Lagrange Multiplier 이론 정리 (0) | 2023.07.29 |
| Exponential Family 개념 정리 (0) | 2023.06.24 |
| LDA(선형판별분석) 에 대한 완벽 개념 (0) | 2023.06.04 |