Lagrange Multiplier 이론 정리

아맞다 시리즈 4번째. 오늘은 머피의 머신러닝 8.5 장에 나오는 Lagrange에 대해 본인이 소화한 대로 정리해 볼 것이다. 라그랑지 승수는 SVM을 설명할 때나 exponential family에서 엔트로피를 설명할 때, MLE에 대해 설명할 때에도 나오는 방법이다. 라그랑지와 더불어 KKT condition의 개념까지 정리해보고자 한다.

 

참고 : 머피의 머신러닝 

 

 

---

1. Lagrange Multiplier(라그랑지 승수)  

Constrained optimization

라그랑지 승수를 어떤 경우에 사용하는지 이해하기 위해선 constraint optimization에 대한 이해가 필요하다. 한국어로 직역하면 '억제 최적화'가 된다. optimizer function을 구했는데, 특정 조건을 만족해야 한다면 이 특정 조건이 constraint라 할 수 있다. 예를 들어 1/2(w*x - y)**2가 목적 함수이며, 이 함수를 minimize 해야 최적화하는 것이라고 하자. 그런데 w는 무조건 0과 0.3 사이여야 한다고 한다. 그러면 이 0 <=w <=0.3이라는 조건이 constraint가 된다. 

 

 

constraint에는 크게 2가지 종류가 있다. 하나는 equality constraints, 다른 하나는 inequality constraints다. equality constraint는 식으로 나타냈을 때 h(x) = 0 으로 나타낼 수 있는 constraint(h(x))를 의미한다. 반대로 inequlity 함수는 h(x) <= 0을 만족한다. 

 

아래 그림을 확인해보자. 파란 선이 constraint, 빨간 함수는 목적 함수라고 가정한다. 왼쪽 그림의 constraint는 θ1 +  θ2 - 1 = 0을 만족하므로 equality constraint다. 반면 오른쪽의 constraint는 |θ1| + |θ2| - 1 <= 0으로 inequality constraint다. 

 

equality / inequality constraints

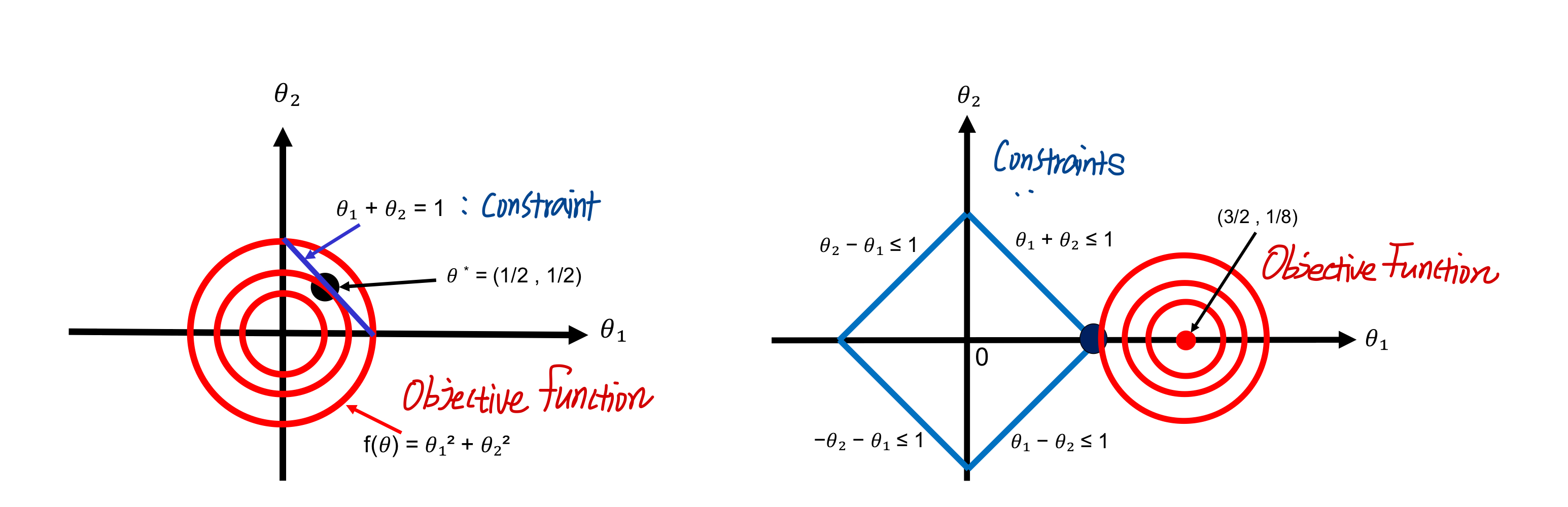
우리는 constraint을 만족시키는 목적함수의 값을 구해야 하고, 그림에서와 같이 목적함수와 constraint함수가 만나는 지점을 찾는 것과 같다. 그러려면 constraint 수식도 목적함수(ex. loss function)에 녹여서 하나의 식으로 만들면 편할 것이다. 이를 위한 것이 라그랑지 승수다. 

 

 

 

Lagrange Multiplier

equality constraint h(θ)=0이 있다고 가정해 보자. 이 함수와 목적함수의 기울기값이 같은 지점을 찾아야 한다. 이걸 수식적으로 풀어내니 ∇h(θ)이 h(θ)와 수직임을 만족하는 것과 같아지는데, 그 과정을 한 번 설명해 보겠다.

 

1. θ의 근처에 있는 θ+ε라는 값이 있다고 가정하자. 입실론 ε은 매우매우 작은 값이다. θ와  θ+ε를 미분식으로 풀면 아래 식과 같이 정리할 수 있다. 

equality constraint h

2. 추가로 ε가 매우 작은 값이기 때문에 h(θ+ε) == h(θ)를 만족해야 한다. 그러면  ε * ∇h(θ) == 0이 되어야 한다. 

3. ε은 constraint surface와 평행하기 때문에, 따라서 ∇h(θ)는 constraint surface에 수직해야 한다. 

 

 

 

이제 어떤 목적 함수 L(θ)을 minimize하는 최적화 식을 생각해 보자. L도 최솟값을 찾아야 함과 동시에 constraint인 h(θ) = 0 도 만족해야 하는 상황이다. L(θ)와 constraint가 만나는 지점을 찾는 것이니, ∇L(θ)도 constraint surface에 수직일 것이다. 그렇다면 우리가 아는 건  ∇h(θ)와 ∇L(θ)이 constraint surface에 수직이란 것이다. 따라서 목적함수 L와 h은 아래 식을 만족해야 한다. 이때 람다 λ가 Lagrange Multiplier이다. 

lagrange multiplier 설명

 

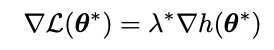
이를 통해 새로운 최적화 함수를 정의할 수 있다. L(θ)에 ∇L(θ)을 더한 새로운 Lagrangian을 목적 함수로 사용할 수 있게 되었다! 

 

Lagrangian

당연히 이 식의 stationary point에서는 다음과 같이 h(θ) = 0인 constraint와 L과 h의 기울기가 평행함을 만족한다.

lagrange multiplier 설명2

 

 

 

 

2. KKT Condition

위에서는 equality constraint h(θ)를 활용해 라그랑지 승수를 이해했다. 이번에는 inequality constraint g(θ)에 대해 전개해보자. inequality constraint는 0보다 작거나 같음을 전제했기 때문에 g(θ) <= 0 을 만족해야 한다. 이번 최적화 함수는 unconstrained problem으로 접근할 수 있다. g(θ) > 0 인 경우 값을 무한대로 보내버리는 것이다. 

 

 

inequality constraint를 위한 식

 

이런 함수를 설계하게 되면 미분이 불가능하단 단점이 있다. g(θ) == 0일 때처럼 말이다. 그래서 이 식을 아래와 같이 다시 구성하고 싶어 진다.  

lagrangian with inequality constraint

이 식또한 g(θ) 가 0 이상이면 무한히 L(θ)이 u와 비례하여 커지고(~= 위에서 무한히 커진 것과 유사), 그렇지 않으면 L(θ) 값과 동일하다. 

 

 

 

여기까지 우리는 equality constraint이 있을 때의 lagrangian과 inequality constraint이 있을 때의 lagrangian을 각각 알았다. 

lagrangian with equality constraint	lagrangian with inequality constraint
Lagrangian	lagrangian with inequality constraint

 이제 Lagrangian을 일반화할 수 있을 것 같다. L(θ)에 equality constraint이 몇 개든 h(θ)와 라그랑지 승수를 곱한 값을 더하고, inequality constraint 수만큼 g(θ)와 u를 곱한 값을 더한 것이 된다! 바로 아래 식처럼 말이다.

Generalized Lagrangian

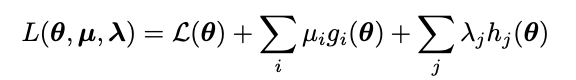
이 식의 stationary point는 세 함수의 기울기 합이 0임을 보이게 된다. 

 

여기서 KKT(Karush-Kuhn-Tucker) condition의 정의가 나오게 된다. KKT 조건을 받는다면 다음 식을 조건으로 만족해야 한다. 

 

 

이 조건은 u와 g의 조건에 대한 내용으로, equality constraint에 대한 lagrange를 풀 때를 생각해 보면 된다. g 또한 constraint이기 때문에 아래 식에서 h가 만족했던 수식을 동일하게 적용받기 때문이다. 

lagrange multiplier 설명

 

 

 

 

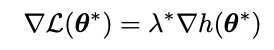
3. 활용 예시

라그랑지 승수에 대한 개념을 알았으니, 다양한 ML 이론에서 어떻게 활용되는지를 알아보자.

MLE (Maximum Likelihood Estimation)

MLE에 대한 글을 작성할 때 categorical distribution의 loss 함수를 구하는 쪽에서 라그랑지 승수를 사용했었다. 사용된 이유는 categorical distribution에서의 확률값 θ 의 합이 1을 만족해야하는 constraint가 있기 때문이다. equality constraint가 있는 상황에서 최적화를 하기 때문에 이 constraint를 라그랑지 승수를 사용함으로써 고려할 수 있게 된다. 

Lagrange Multiplier with categorical MLE

https://hi-lu.tistory.com/entry/%EC%95%84-%EB%A7%9E%EB%8B%A4-MLE 

[아 맞다] MLE

 

 

 

SVM (Support Vector Machine)

약한 매운맛 SVM글에서 깊게 다루진 않았지만, SVM에서도 lagrange multiplier가 사용된다. SVM의 constraint로 사용하는 N개의 변수를 inequality constraint로 간주하고, 이 억제 변수들을 강화하기 위해 라그랑지 승수를 사용한다. 

SVM dual with inequality constraint

 

 

SVD (Singular Value Decomposition)

고윳값분해 SVD에서는 x(T)Ax 꼴의 SVD를 만족하는 벡터가 있을 때 이 벡터 최적화문제에서 사용할 수 있다. x자리에 들어가는 데이터는 SVD에서 eignevector(고유벡터)의 자리이고, eigenvector는 크기가 1인 벡터다. 그렇기 때문에 ||x|| == 1이라는 equality constraint를 만족하며 최적화를 할 수 있게끔 라그랑지 승수를 이용할 수 있다. 

 

Lagrange Multiplier in SVD

 

---

오늘은 ML 이론을 공부하면서 자주 등장하는 라그랑지 승수에 대한 개념을 바삭바삭하게 정리해 보았다. 머피의 머신러닝을 따라가다 보면 하나의 개념이 다른 이론들을 설명하는 데에 쓰이곤 한다. 그럴수록 더 기초와 이론을 놓지 말고 계속 공부해야 한다는 생각이 든다.