[Paper] DPO 논문 리뷰

오늘 다뤄볼 논문은 Direct Preference Optimization : Your Language Model is Secretly a Reward Model이다. 최근 LLM에서는 RLHF(Reinforcement Learning with Human Feedback) 방법론을 자주 접목시켜 모델을 학습하는데,  DPO는 이 RLHF 계열의 알고리즘을 업데이트한 내용이다. 

 

 

논문 : https://arxiv.org/abs/2305.18290

Direct Preference Optimization: Your Language Model is Secretly a Reward Model

 

---

 

1. 들어가면서

LLM(Large Language Model)이 발전하면서 human label을 통해 학습하는 방법론이 최근 대두되고 있다. LLM을 학습하기 위한 큰 흐름을 보자면 1) LM에 인간이 라벨링을 한 데이터로 모델 finetuning을 하고, 2) finetuning 과정에서 RLHF를 쓰고 있다. ChatGPT도, LLAMA2도 RLHF 기반의 학습으로 언어모델을 완성시켰다.

 

오늘은 모델의 finetuning 과정에서 사용하는 RLHF를 대신한 DPO(Direct Preference Optimization)에 대해 알아본다. DPO는 PPO와 같은 강화학습 policy를 사용하지 않고(reward modeling이 없음), reward 함수와 본 policy만을 매핑하여 human preference data에 최적화할 수 있다고 논문에서 말한다. RLHF로 finetuning한 모델에 비해서 요약, single-turn 문제에서 더 좋은 성능을 보였다. 

 

그림 1.RLHF vs DPO

 

 

 

 

2. RLHF

RLHF는 reward model 인간이 선호도(human prefrence)를 매긴 데이터셋을 이용해서 강화학습을 통해 이 선호도를 학습하게 된다. 1)높은 reward를 주는 데이터에 가깝게 학습될 수 있도록 LM을 최적화함과 동시에 2) LM이 기존에 return하는 policy에서 너무 멀어지지는 않게 제약을 준다. 제약을 주는 방식은 KL divergence를 이용한다. 그림 1의 왼쪽과 같이 강화학습을 이용한 rewrad 모델과 기존 언어모델(LM policy)을 서로 잘 얼라인해야 하는 구조다. 

 

 

finetuning방법은 크게 3가지로 나뉘는데, 첫번째인 SFT(supervised Fine Tuning)은  pretrained LM을 학습 데이터셋으로 간단히 학습시키는 것이다. 

 

Reward Modeling Phase

두번째부터 RLHF가 등장한다. RLHF의 목적을 복기하자면 SFT로 학습한 모델이 인간의 마음에 들게끔 잘 답변하게 튜닝하는 것이다. 그러기 위해선 SFT에서 어떤 input에 대해 답변한 output들에 점수를 메겨, 가장 인간의 마음에 든 output이 높은 점수를 받고 그렇지 않으면 낮은 점수를 받게끔 reward를 설정해야 한다. 

 

x라는 prompt를 모델의 input으로 준다고 가정하고, SFT로 학습한 모델로 하여금 2개의 output을 생성해내보자. 2개의 output y1, y2를 얻었다. 

 

 

이제 '인간'이 등장한다.

y1과 y2 중 어떤게 올바른 output인지 점수를 매긴다. 주어진 output들에 대해 reward를 주는 것이다. y1,y2 중 인간이 선호하는 답변을 yw, 비교적 비선호하는 답변을 yl라고 하자. 지금은 점수(reward)를 사람이 줬지만 이를 통해 reward model을 설계해야 한다. 주어진 reward를 '학습'에 이용하기 위해 새로운 모델을 만든 것이다. 이 latent reward model을 r(y,x)라고 표현한다.

 

r을 정의하는 데에는 여러 알고리즘이 있지만 주로 BT(Bradley-Terry) 방법을 사용하며, 수식은 아래와 같다. y1의 reward가 더 높을 확룔을 확률모델로 정의한 것이다. 

Bradley-Terry

 

 

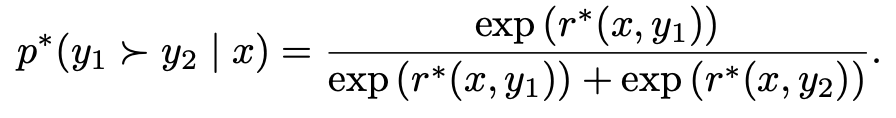
수식을 보니 학습 방향이 보인다.

P(y1 > y2 |x)는 y1의 reward가 y2의 reward보다 높을확률이다. 만약 인간이 y1에게 y2보다 높은 reward를 부여했다면 우리는 P(y1 > y2 |x)가 P(y2 > y1 |x)보다 높은 확률을 가지길 바랄 것이다. 이렇게 학습될 수 있도록 NLLoss를 아래와 정의할 수 있다. (선호답변은 yw, 비선호 답변은 yl이었다.)

RLHF reward model loss

 

reward model rϕ의 초기 세팅은 SFT모델의 마지막 linear layer output과 같다. human feedback를 받은 데이터를 통해 rϕ은 점점 업데이트될 것이다. 

 

 

RL Fine-Tuning Phase

reward loss로만 학습시키기에는 불안정성이 있다. reward model이 말하는 최적화된 답변과 현재 sft로 파인튜닝해서 나온 최적화된 답변이 너무나도 다르면 문제가 있기 때문이다. 그렇기 때문에 reward loss에 constraint를 추가해준다. 

 

 

KL dievergence는 두 확률이 같을수록 0에 수렴하는 특징이 있다. 새로 학습한 π와  기존 initial model인 πref간의 큰 차이가 없다면 constraint는 0에 가까워질 수 있다. 이 KL term을 통해 언어모델이 너무 reward에 빨려들어가지 않게 조절할 수 있다. 최종 loss는 미분이 안되기 때문에 강화학습 방법론 중 PPO를 통해 학습한다. 최종 loss를 강화학습에 학습할 reward로 바라보고 최적화하는 형태다.

 

 

3. DPO(Direct Perference Optimization)

DPO는 '최종 loss를 reward로 받아서 ppo로 업데이트'하는 과정을 없앴다. RLHF의 reward modeling phase에서 바로 언어모델을 학습하는 형태로 변형시킨다. 그래서 reward modeling을 preference modeling 과정으로 치환한다. (reward는 강화학습에서 쓰는 단어이기 때문에, DPO는 강화학습을 쓰지 않는다!를 강조하기 위해 preference modeling이라 명명한듯하다.)

 

 

DPO 유도수식

만지작 1. optimal policy π 구하기

RLHF의 RL Fine-Tuning Phase에서 구한 최종 loss를 가져와서, DPO에 맞게 만지작해보자. 

DPO 수식 1.

여기서 Z는 아래와 같다. 업데이트 중 모델인 π와는 무관한 partition function이다. πref와 x로 이루어져있지만 π와는 무관하단 점을 기억해야 한다. 

 

 

위 과정을 통해서 새로운 optimal policy π*를 다음과 같이 쓸 수 있다. 이는 DPO 수식1의 파란 형광펜 부분과 같다. 이 term을 maximize하면 전체 Loss를 minimize하는것과 같기 때문이다. 

 

 

π*를 DPO 수식1에 다시 대입해보자. 그러면 min E 내부의 term이 log π(y|x) / π*(y|x) - log Z가 된다. E π(y|x)이기 때문에 수식을 풀면 KL(π| π*)가 된다. Z는 어차피 π와 관련이 없었고, 우리는 π를 최적화하기 위한 수식을 구하는 것이기 때문에 Z 관련 term은 날아간다. 그러면, π이 π*에 근접할 때 loss가 가장 작다는 의미가 된다. 

 

따라서 π와 π*는 아래와 같다. 

DPO 수식 2.

 

 

만지작 2. reward model 다시 쓰기

만지작 1에서 도출한 바에 따르면 최적의 π*와 기존 π는 모두 아래와 같이 중간수식 1로 표현가능했다. 

중간수식 1

 

중간수식 1의 양 변에 log를 취하고 reward r(x,y)를 좌변에 옮기면 아래 중간수식 2를 도출가능하다. policy를 통해 reward를 나타낼 수 있음을 보였다. 

중간수식 2

 

이제부터 RL Modeling Phase에서 사용했던 Bradley-Terry model의 r와 r* 자리에 각각 중간수식 2를 대입해본다. DPO만의 새로운 preference(reward) model을 도출했다. 

중간수식 3. 새로운 reward model.

 

RLHF에서와 동일하게 y1,y2를 human feedback로 인해 선호 비선호 답변으로 매긴 yw, yl로 중간수식 3에 대입한 후 NLL로 나타낸다면, 아래와 같이 최종 DPO loss를 구할 수 있다! 따로 reward model function(RLHF에서의 rϕ)을 두지 않고 직접적으로 언어 모델의 loss를 도출했단 점이 이 논문의 차별점이다.

DPO loss

 

 

4. Theoretical Analysis of DPO

DPO에서 reward model이 필요없단 주장을 뒷받침하는 근거는 '내 언어모델은 이미 reward model역할을 하고 있다' 이다. 이를 천천히 증명해볼 것이다. 즉 reward 함수가 언어모델 policy로 충분히 도출될 수 있다는 것이다. 이를 증명하기 위해 두개의 명제가 필요하다. 

명제 1. Bradley-Terry 모델에 근거한 두 reward 함수는 같은 클래스(c)에서 같은 preference distribution을 따른다.
-> Pπ(c) = Pπref(c)

명제 2. 강화학습에서 같은 클래스(c)에 대한 두 reward function의 optimal policy는 같다. 
-> π r(x,y) = πref r(x,y)

정의1. r(x,y)와 r'(x,y)가 어떤 함수 f(x)에 대해서 r(x,y) - r'(x,y) = f(x)를 만족하면 r과 r'는 동일하다.

 

명제 1은 probability를 단어 토큰 y1,...yk에 대한 랭킹(τ)을 reward라고 생각해보자. probability를 softmax로 가정하고, 정의 1을 사용해 r'(x,y)자리에 r(x,y)+f(x)를 대입하면 쉽게 증명가능하다. 이를 통해 probability를 계산하는 중에 어떤 식이 생략될 수 있다는 것을 알 수 있고, 즉 preformance model에서 constraint를 주입해도 괜찮다는 결론이 나올 수 있다.

증명 : 두 reward function의 distribution은 같다.

 

 

명제 2는 동일한 클래스에서의 모든 reward function들이 하나의 optimal policy를 가진다는 의미이다. 이또한 r'(x,y) = r(x,y) + f(x)를 이용하면 아래와 같이 쉽게 나온다. 

증명 : 두 reward function의 policy는 같다.

 

 

이제 우리는 두 명제를 통해 reward model r(x,y)가 모델의 policy인 πr를 통해 표현할 수 있음을 보일 것이다.(RLHF은 πr을 최적화하기 위해 PPO를 쓰지만, DPO에서는 πr을 단지 언어모델의 policy π로 표현가능했다.) DPO 설명에서 등장한 DPO 수식 2.을 다시 가져와서 의미를 살펴보자. 이때의 πr은 DPO의 최적의 policy이자 reward function을 의미했다. 

 

r(x,y)와 πr에 대해 f(x)(x,y) = r(x,y) - πr(y|x)가 성립한다면(정의1), r과 π에 대한 두 명제도 성립할 것이다. 임의의 projection f에 대해 아래 식을 가정해보자. (f에 βlogZ가 있나 보다.)

DPO reward model 증명1

 

 

여기서 우리는 위 식을 만족하는 f가 존재하는지만 알면 r(x,y)와 모델의 policy π가 동일하다 말할 수 있다. 그리고 만족하는 f가 당연히 있다. DPO 설명의 중간수식 1 에 해당하는 식을 유심히 들여다보자. 생긴게 너무너무 DPO reward model 증명1 와 닮았다! 

중간수식 1

 

즉 f는 π에 대한 식이다. 어떠한 f에 대해 DPO reward model 증명1 이 성립함을 보인 것이다.

 

 

따라서, 언어모델은 그 자체로 reward model의 역할을 하고 있다. 여기서 추가로 f 자체로도 r(x,y)의 역할을 할 수 있긴하다. reward 함수의 log 값에 Z라는 constraint를 더한 것(명제 1에 의하면 constraint를 임의로 주입해도 reward함수의 probability는 동일했다)이기 때문이다.

 

 

5. Experiment

실험 내용중 특별히 볼 만한 것을 하나 꼽자면 아래와 같다. 첫째로 PPO(RLHF)를 적용한 모델은 KL이 일정이상 커지면 해당 policy에 reward가 아예 계산되지 않는 것에 반해, DPO를 적용한 모델은 KL에 independence하게 reward를 주고 있음을 볼 수 있다. 

 

 

그리고 RLHF에 비해 DPO가 temperature에 대해 robust하다고 한다. reported된 성능은 솔직히 RLHF와 큰 차이는 없어보인다. 

 

 

 

 

---

 

블로그에는 정말 굉장히 오랜만에 논문 리뷰를 하는 듯하다. DPO는 RLHF를 쓸 때에 비해 computation cost나 구현이 비교적 쉽지만, 학습한 데이터 외에선 취약하다(OOD. Out oOf Distribution)는 문제를 갖고 있기 때문에 현업에 바로 적용하기에는 어느정도 성숙되어야 사용가능해 보인다. 그래도 강화학습을 접목시킨 LLM 흐름에서 나름 신선하다고 생각한다. 

 

DPO를 통해 RLHF 알고리즘도 제대로 복습하고, 이해도도 좀 더 올라간 거 같아 좋다.